Пусть есть объект, который движется со некоторой скоростью из пункта A в пункт В, расстояние между которыми проходится за некоторое время.
Обозначения:

- общее обозначение пути

- конкретный путь, равный расстоянию между пунктами A и B

- некоторое приращение пути за приращение времени


- величина пройденного пути на момент времени


- дифференциал пути

- дифференциал пути в момент времени


- общее обозначение времени

- конкретное время, за которое было пройдено расстояние между пунктами A и B

- некоторое приращение времени

- некоторый момент времени

- дифференциал времени

- дифференциал времени в момент времени


- общее обозначение средней скорости

- конкретная средняя скорость, было пройдено расстояние между пунктами A и B

- общее обозначение мгновенной скорости

- конкретная мгновенная скорость в момент времени

Это всё хорошая попытка, но всё это надо
выкинуть к чертям.
Начать надо с физической ситуации. Рассмотрим движение
точки,
вдоль одной линии, и при этом
неравномерное (но монотонное). С этими оговорками, можно сопоставить физической ситуации математическую модель.
Далее, математическая модель такого движения. Возьмём за параметр время

Всё движение происходит на каком-то промежутке времени
![$t\in[t_A,t_B].$ $t\in[t_A,t_B].$](https://dxdy-03.korotkov.co.uk/f/a/3/2/a32cb00a0ed60efe92d80ec13e56ff6e82.png)
Само движение описывается
функцией 
Это очень важно: разобраться, где у вас отдельные
числа, а где
функции. Число - это не то же самое, что "постоянная".
Постоянная функция - это тоже
функция, но такая, которая принимает одно и то же значение. А число не является функцией, в него нельзя подставить какой-то аргумент. Только постоянные функции имеют право обозначаться

Замечание по нотации. Довольно часто одни и те же вещи обозначаются по-разному. Реже в математике, и чаще в физике. Это нормально, но за этим надо следить. Недопустимо другое: чтобы разные вещи обозначались одинаково. Впрочем, такое тоже бывает, если по контексту понятно, какой смысл имеется в виду.
Например, функцию  очень часто обозначают в физике просто
очень часто обозначают в физике просто 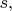 чтобы не громоздить обозначений. Отдельные значения этой функции тоже можно называть какими-то специальными значками, например,
чтобы не громоздить обозначений. Отдельные значения этой функции тоже можно называть какими-то специальными значками, например, 
В этом разделе математики есть одно "неудачное" обозначение, когда одинаково обозначаются разные вещи. А именно,  может обозначать целиком всю функцию, если буква
может обозначать целиком всю функцию, если буква  не фиксирована в каком-то значении, а остаётся просто переменной. Но если где-то начали говорить о каком-то конкретном моменте
не фиксирована в каком-то значении, а остаётся просто переменной. Но если где-то начали говорить о каком-то конкретном моменте  то это же обозначение
то это же обозначение  будет обозначать одно конкретное число - то значение функции, которое она принимает в этот момент, при этом аргументе.
будет обозначать одно конкретное число - то значение функции, которое она принимает в этот момент, при этом аргументе.
И совсем мелкое замечание. Большие буквы  выглядят "по-школьному". Принято для пути, скорости и времени использовать маленькие буквы
выглядят "по-школьному". Принято для пути, скорости и времени использовать маленькие буквы  потому что в физике бывает площадь, объём, период, энтропия, температура и так далее. Иногда пишут большую букву, если маленькая уже занята.
потому что в физике бывает площадь, объём, период, энтропия, температура и так далее. Иногда пишут большую букву, если маленькая уже занята.
Итак, пока математическая модель состоит из:
 лежащей в промежутке
лежащей в промежутке ![$[t_A,t_B]$ $[t_A,t_B]$](https://dxdy-01.korotkov.co.uk/f/c/1/a/c1a28229916aa6e8962db5b9b3ce092682.png) ;
;
 принимающей значения в промежутке
принимающей значения в промежутке ![$[0,s_{AB}],$ $[0,s_{AB}],$](https://dxdy-01.korotkov.co.uk/f/8/6/3/8634deefb9e7ebabc0e3b36b5a50918b82.png) причём
причём 
И всё, достаточно, не надо городить лишнего. Зато видно, что с чем как связано.
Теперь можно от этой функции взять производную (мы считаем, что функция дифференцируема всюду на промежутке), и обозначить её новой
функцией:
Внимание: здесь не вводятся никакие обозначения

! Здесь используется обозначение производной "по Лейбницу"

Здесь пока всё понятно?
Отдельно, можно посчитать
число (из других
чисел)
Здесь всё понятно?
На этом пока остановимся, потому что здесь всё должно быть кристально ясно, и без лишних обозначений, без суеты и без путаницы.



