Опишите пространство элементарных исходов, соответствующее броску двух монеток, и случайные величины

и

на нем (пусть индикаторы выпадения орла на первой и второй монетках).
Ну это как посмотреть. Если сразу как для двух монеток, то пространство элементарных исходов будет состоять из

элементов - собственно все сочетания на первой и второй монетки. Тогда и случайные величины нужно определить для каждого из этих четырех исходов. Но я рассматриваю не их совместное бросание, а просто две монетки чтобы были независимые случайные величины. Соответственно пространство каждой это два исхода орел или решка и соответственно два значения для случайных величин

и

. И затем перемножаю их и хочу посчитать математическое ожидание произведения.
Вот собственно формулы что я приводил в первом сообщении это из "Конкретной математики" Кнута, Поташника доказательство формулы мат ожидания произведения независимых величин. Еще раз - вот буквально цитата части доказательства:

Мне не понятны эти две формулы, точнее как это они равны. Какие там такие пространства

, и

,
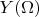
чтобы это было верно?



