Математическое ожидание произведения

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[mihaild]

bayah в сообщении #1326188 писал(а):

а просто две монетки чтобы были независимые случайные величины

Приведите определение независимости случайных величин в терминах функций, пространств и мер. В частности, должны они быть определены на одном пространстве или нет?

bayah в сообщении #1326188 писал(а):

И затем перемножаю их

Как вы перемножаете функции с разными областями определения?

[bayah]

mihaild в сообщении #1326230 писал(а):

Приведите определение независимости случайных величин в терминах функций, пространств и мер. В частности, должны они быть определены на одном пространстве или нет?

Я могу привести такое определение.
Величины $X$ и $Y$ независимы если для них выполняется:
$P(X=x, Y=y) = P(X=x) \cdot P(X=x)$
для всех $x \in X$ и $y \in Y$.

mihaild в сообщении #1326230 писал(а):

Как вы перемножаете функции с разными областями определения?

Почему с разными? С одной и той же областью определения $\Omega$

[mihaild]

bayah в сообщении #1326250 писал(а):

Величины

Определение случайной величины дать можете?

bayah в сообщении #1326250 писал(а):

Почему с разными?

Ну вы же пишете

bayah в сообщении #1326188 писал(а):

пространство каждой

[bayah]

mihaild в сообщении #1326251 писал(а):

Определение случайной величины дать можете?

Случайная величина есть функция $f: \Omega \to \mathbb R$

mihaild в сообщении #1326251 писал(а):

Ну вы же пишете
bayah в сообщении #1326188

писал(а):
пространство каждой

Ну они же одинаковые эти пространства...

В общем, вы хотите сказать, что нужно так:
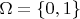
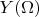
Если есть события бросания монеты на вероятностном пространстве $\Omega = \{0, 1\}$, и случайные величины $X(\Omega)$ - выпадение на первой монете и $Y(\Omega)$ - на второй, то определяя мат ожидание произведения таких величин как
$E(XY) = \sum\limits_{\omega \in \Omega} X(\omega)Y(\omega)P(\omega)$
это заведомо определяет что величины зависимые (так как $X = Y$ при всех $\omega$ )?
Тогда чтобы это были независимые величины нужно определить вероятностное пространство например так:
$\Omega = \{(0,0), (0,1), (1,0), (1,1)\}$ и случайные величины $X((i, j))=i$ и $Y((i, j))=j$.

Тогда это становится корректным равенством:
$E(XY) = \sum\limits_{\omega \in \Omega} X(\omega)Y(\omega)P(\omega) = \sum\limits_{x \in X(\Omega), y \in Y(\Omega)}xyP(X = x, Y = y)$

?

[mihaild]

bayah в сообщении #1326429 писал(а):

это заведомо определяет что величины зависимые?

Да, любые две неконстантные случайные величины на двухэлементном вероятностном пространстве зависимы.

bayah в сообщении #1326429 писал(а):

Тогда это становится корректным равенством:
$E(XY) = \sum\limits_{\omega \in \Omega} X(\omega)Y(\omega)P(\omega) = \sum\limits_{x \in X(\Omega), y \in Y(\Omega)}xyP(X = x, Y = y)$

Это равенство выполнено вообще всегда (для конечных вероятностных пространств).

bayah в сообщении #1326429 писал(а):

Ну они же одинаковые эти пространства...

А чтобы говорить о независимости, вам нужны не "одинаковые" пространства для величин, а одно и то же для обеих.

[Someone]

Если случайные величины $X$ и $Y$ определены не на одном и том же вероятностном пространстве, а на "одинаковых", то мы не можем использовать эти величины вместе из-за того, что у них разные области определения. В частности, мы не можем рассматривать величины $X+Y$ или $XY$, потому что, например, сумма функций $X+Y$ определяется как $(X+Y)(\omega)=X(\omega)+Y(\omega)$, где $\omega$ во всех трёх случаях одно и то же, а не "одинаковые".

[bayah]

mihaild в сообщении #1326498 писал(а):

А чтобы говорить о независимости, вам нужны не "одинаковые" пространства для величин, а одно и то же для обеих.

Someone в сообщении #1326505 писал(а):

Если случайные величины $X$ и $Y$ определены не на одном и том же вероятностном пространстве, а на "одинаковых", то мы не можем использовать эти величины вместе из-за того, что у них разные области определения.

Ну все, вроде дошло, спасибо).