Пусть

-- группы, заданные образующими и соотношениями

.
Как с помощью образующих и соотношений

задать:
1)

2)

3)
![$G_1/\left[ G_1, G_1 \right]$ $G_1/\left[ G_1, G_1 \right]$](https://dxdy-04.korotkov.co.uk/f/3/d/9/3d9e3f09fe14b80d070de7ea45d5e8a982.png)
1) Интуитивно ясно, что

. Но доказать я это не могу.
2)
![$S = S_1 \sqcup S_2, \, R = (R_1 \sqcup R_2) \cup \lbrace [g_1,g_2] | g_1 \in S_1, g_2 \in S_2 \rbrace $ $S = S_1 \sqcup S_2, \, R = (R_1 \sqcup R_2) \cup \lbrace [g_1,g_2] | g_1 \in S_1, g_2 \in S_2 \rbrace $](https://dxdy-02.korotkov.co.uk/f/1/c/9/1c9555642461f430537a690d3109f51782.png)
.
Доказать можно следущим образом:
![$G_1 * G_2 /[G_1, G_2] \simeq G_1 \times G_2$ $G_1 * G_2 /[G_1, G_2] \simeq G_1 \times G_2$](https://dxdy-01.korotkov.co.uk/f/c/b/8/cb81910a87a085ef3a1d9601f868fbed82.png)
, поскольку
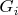
в эту факторгруппу естественным образом вкладываются, порождают её, и являются в ней нормальными подгруппами (всё неочевидное проверяется непосредственно). Если с пунктом (1) я угадал правильно, то само утверждение следует из сказанного, (1) и
этого факта.
3) Из рассуждений, аналогичных последней части п.2, ясно, что
![$S = S_1, R=R_1 \cup \lbrace [g,g'] | g, g' \in S_1 \rbrace$ $S = S_1, R=R_1 \cup \lbrace [g,g'] | g, g' \in S_1 \rbrace$](https://dxdy-02.korotkov.co.uk/f/1/b/7/1b7c295a12c5a3e4d59ebeba5fd18ff382.png)
Помогите с первым пунктом, пожалуйста!



