136. Доказать, что если последовательность

(

) ограничена и

, то частичные пределы этой последовательности расположены всюду плотно между ее нижним и верхним пределами:

и

, то есть любое число из отрезка
![$[l, L]$ $[l, L]$](https://dxdy-04.korotkov.co.uk/f/3/0/f/30ffe1fe38b990a85d2f8c0893c0e59582.png)
является частичным пределом данной последовательности.
Пусть некоторая точка
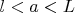
не является частичным пределом данной последовательности. Тогда существует

такое, что начиная с некоторого


(иначе можно уменьшая

построить подпоследовательность, которая сходится к

). Откуда

или

. Поэтому разность любых двух

и


("перешагнуть" через

последовательности придется т.к. для любых

найдутся

, которые лежат сколь угодно близко к

и к

), что противоречит

Будет ли засчитано такое решение на экзамене? Сомнение у меня вызывает "перешагивание". Возможно есть и другие проблемы. Подскажите, пожалуйста, как исправить мое решение.



