Насчет ранг = 0, Вы видимо правы.
В книге ранг кривой для меня сложен, поэтому я брал из Википедии "Рангом эллиптической кривой

называется минимальное число рациональных точек бесконечного порядка из теоремы Морделла" и что "любая точка на эллиптической кривой представляется в виде:
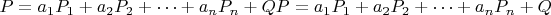
"
Если акцентировать на "любая", то вроде сходится. На любой кривой справедливо

", а в нашем случае их всего две.
Наверно и со сложением точек меня сбило с толку то что в формулах для координат

и в их и моей нормальных формах

, а в исходной

, то есть она из исходных точек.
Остальное, мелочи.
Так что, еще раз спасибо. Похоже все вопросы прояснились.



