В классическом доказательстве оценки интеграла Виноградова

основную роль в понижении порядка оценки играет, как я понимаю, лемма о количестве сумм разных степеней чисел разных интервалов, которые (суммы) лежат в заданных не очень больших интервалов.
Строго это формулируется так (привожу чуть изменённое изложение Карацубы, но у Виноградова так же, только константы другие):
Цитата:
Пусть

и пусть

пробегают разные интервалы
![$v_i \in [X_i,Y_i]$ $v_i \in [X_i,Y_i]$](https://dxdy-03.korotkov.co.uk/f/e/7/0/e70c7fe730559087c1b92c700c1968a982.png)
, каждый длины

, которые отстоят друг от друга не менее чем на

, причём

. Тогда количество их наборов, при которых суммы

лежат в заранее заданных интервалах длин

не превышает

Какая там

- не суть важно: главное, что от тривиальной оценки через степень неограниченно растущего

мы переходим к оценке, зависимой уже только от

.
Доказательство теоремы проводится через конструирование СЛАУ и анализ возникающих из неё определителей Вандермонда, то есть существенно использует то, что мы работаем с последовательными степенями чисел.
При этом после всех технических преобразований, связанных с матрицей Вандермонда, оказывается, что главной сутью этого действа является зависимость вариабельности

от значения

, где
![$x_i \in [X_i;Y_i]$ $x_i \in [X_i;Y_i]$](https://dxdy-02.korotkov.co.uk/f/5/d/f/5df5f2b822479d76f5159311f74f3f9f82.png)
. То есть важна именно отдалённость интервалов друг от друга.
И, действительно, задумавшись, я понял, что это очень интуитивно - если какая-то функция

(в нашем случае

) выпукла (и сильно выпукла), а интервалы, в которых живут
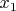
и
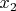
, сильно отдалены друг от друга, то система

имеет очень-очень мало решений (может быть, даже одно) - ведь одинаковые разнонаправленные подвижки переменных
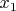
и
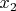
, сохраняющие первое уравнение, не сохранят второе, ввиду разницы производной

на двух отдалённых участках.
То же рассуждение уместно для произвольного количества интервалов и функций.
В связи с этим возникает вопрос - а возможно ли заменить в изложенной в начале лемме обычные степени

на произвольные выпуклые функции

с каким-то строгим требованием выпуклости типа (например, просто обобщая)

?
И возможно ли сделать это тем же способом через определители, то есть существуют ли общие методы оценки снизу определителей

если известно, что каждая
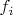
намного (в каком-то смысле) выпуклее предыдущей и расстояние между любыми разными переменными

превышает какое-то заранее заданное число?



