В пособии «ЕГЭ. Высший балл. Математика. Профильный уровень», 2017, автор Ерина Т.М. упорно внедряет некие таблицы с довольно мутным наполнением: оно меняется от задачи к задаче.
Вот одна из них:
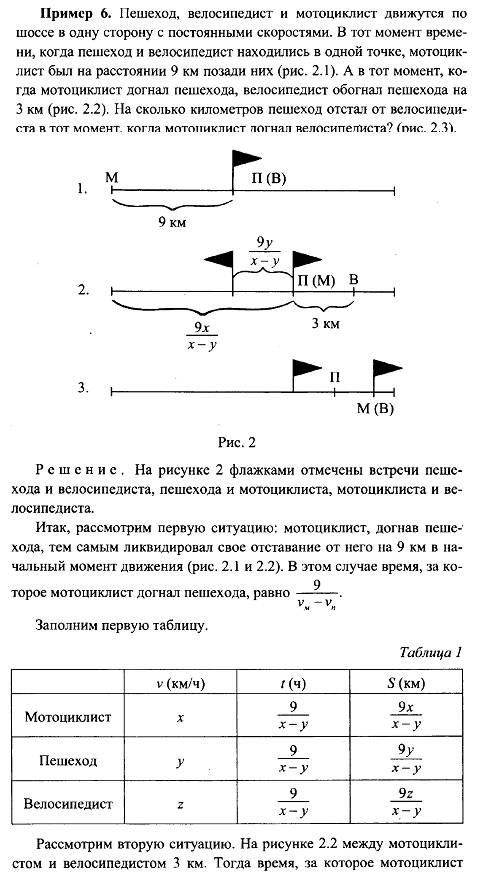


Между тем, задача решается в уме.
Перейдём в систему отсчёта пешехода. Когда мотоциклист проехал 9 км, велосипедист только 3. Их скорости 1:3. Дальше мотоциклист догонял велосипедиста:

, откуда получаем, что велосипедист успел проехать

км. Да между ними изначально было 3 км:

км. – А пешеход-то стои’т!
Принято ругать колмогоровский учебник геометрии 1979 года за громоздкую алгоритмизацию. Как видим, её издержки проявляются и в школьной алгебре.



