Цитата:
Задача 2. Исследовать отображения, построить римановы поверхности

над плоскостью

и разбить

-плоскость на области, соответствующие листам или полулистам

.
А.

исследовать случай

Б.

В.

Г.
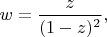
Д.

Е.
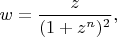
Ж.

З.

И.

Здесь просят уже римановы поверхности строить над

, то есть это римановы поверхности обратной функции

, как я понимаю. (Что такое полулист?)
А.
![$z = n\left(\sqrt[n]{w} - 1 \right)$ $z = n\left(\sqrt[n]{w} - 1 \right)$](https://dxdy-02.korotkov.co.uk/f/d/4/9/d491e75aded6c929aee631cb3c7c8df982.png)
, функция

-листная. Возьмём один лист с разрезом по отрицательной полуоси, на котором аргумент лежит в

(

-лист). На плоскости

этот лист превращается в сектор

,

, при отображении
![$\sqrt[n]{w}$ $\sqrt[n]{w}$](https://dxdy-03.korotkov.co.uk/f/a/1/9/a1903621298a4ca91d11e3ece1daaa7a82.png)
. Дальше точки сдвигаются на единицу влево и расстояние до них потом растягивается в

раз. Это растяжение не влияет на угол раствора сектора, сдвиг тоже, поэтому на плоскость

каждый лист отображается в сектор, центр всех секторов лежит в точке
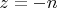
. При

понятно, что
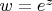
, но увидеть структуру

и

-плоскостей при

из прямого рассуждения выше не получается (точнее, ожидать полосы можно, поскольку центр сектора уехал в бесконечность по действительной оси, но куда переходят внутренности секторов не понятно).
Б.
Имеем
![$\dfrac{z - a}{z - b} = 1 + \dfrac{b - a}{z - b} = \sqrt[n]{w}$ $\dfrac{z - a}{z - b} = 1 + \dfrac{b - a}{z - b} = \sqrt[n]{w}$](https://dxdy-04.korotkov.co.uk/f/b/a/c/bac36614c286b227571aba4018eed2d482.png)
, откуда
![$z = b + \dfrac{b - a}{\sqrt[n]{w} - 1}$ $z = b + \dfrac{b - a}{\sqrt[n]{w} - 1}$](https://dxdy-01.korotkov.co.uk/f/c/0/4/c04bbad39a854371d6534134270474cb82.png)
. Вот здесь уже не видно так сразу, где какие области, кроме того, что
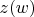
—

-листная функция.
В.
Получаем уравнение

, откуда

,

. Функция двухлистная с двумя конечными точками ветвления

.
Пишем

и

. Разрезаем плоскость по лучам
![$(-\infty, -1]$ $(-\infty, -1]$](https://dxdy-02.korotkov.co.uk/f/1/9/c/19c9426ee43861fbcc74f8b056e5d18682.png)
и

. Назначаем первому аргументу область изменения

, второму

. Напишем

На первом листе верхний берег правого разреза

,

, нижний

,

.
Верхний берег левого разреза

,

, нижний берег

,

.
Приклеиваем второй лист с такими же разрезами, назначая область изменения аргументов
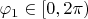
,

.
Верхний берег левого разреза

,

, нижний берег

,

.
Верхний берег правого разреза

,
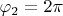
, нижний берег
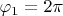
,
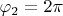
.
Получается следующее для аргументов корня:
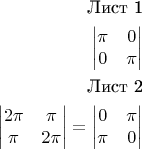
Склеиваем берега соответствующих сторон верхний с нижним и получаем риманову поверхность
. Функция

однолистная, поэтому структура римановой поверхности от прибавления её не поменяется.
Прошу проверить.



