Добрый вечер.
Хочу поставить следующий абстрактный вопрос, который лично мне кажется довольно сложным.
Рассмотрим обычное трехмерное евклидово пространство:

в котором определен обычный метрический тензор:

, так что норма вектора вычисляется по обычному правилу:

, и нашем пространстве действует обычное скалярное произведение:

Тогда группа

может быть определена, как множество биективных преобразований множества

, которые сохраняют скалярное произведение.
Теперь возмутим метрику с помощью малой симметричной матрицы:

, где

, где норма матрицы понимается в смысле какой-нибудь (например, евклидовой) нормы пространства

, и, конечно, возмущение симметрично с тем, чтобы сохранить симметричность скалярного произведения. Можно отдельно рассмотреть вариант когда возмущение сохраняет положительную определенность метрического тензора, а можно этого в целом не требовать.
Тогда интерес представляет группа
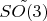
, которая определяется аналогично невозмущенной группе, только теперь надо оставить на месте не старое скалярное произведение, а новое возмущенное. Есть ли связь между

и
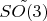
, можно ли как-то сформулировать верное утверждение, что эти группы не слишком сильно отличаются друг от друга?



