Решал одну задачу по комбинаторике, и в процессе выскочило вспомогательное утверждение, которое никак не могу доказать, не используя бесконечные ряды, производящие функции и т.д.
Утверждение такое: для любого натурального


Если бы для

с действительным

верна была бы верна свёртка Вандермонда, то, понятно, искомое бы мгновенно из неё следовало.
Поэтому я прошу либо помощи в доказательстве обобщённой на действительные

свёртки Вандермонда, либо моего утверждения.
Помогите, пожалуйста!
Заранее спасибо.
Комментарий про свёртку Вандермонда.Известно, что для натуральных
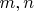
, если

и

, то:
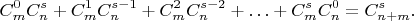
Это - свёртка Вандермонда. если её доказать для действительных

и

(а в нашем случае достаточно для

), то всё будет из неё автоматически следовать, т.к.

.



