Не могу придумать контрпример к 16-й задаче, прошу подсказок.
Пляшу от этого:
Пусть
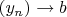
, и

. Тогда

, т.е. последовательность значений

может сходиться к

, даже когда соответствующая последовательность аргументов не сходится к

.
Придумать такую функцию дело нехитрое, но как сделать ее взаимно однозначной?
Возьмем отрезок с центром в т.

. При стремлении

к

с обеих сторон (и слева и справа) значения

стремятся к

только с одной стороны. Как это сделать с сохранением взаимно однозначности

? Есть другой отрезок, с центром, скажем, в точке

. Аналогично, при стремлении

к

с обеих сторон значения

стремятся к

только с одной стороны (не с той, что при

). Эти два отрезка не пересекаются. На иксах вне этих отрезков

.
Пример такой функции

без взаимно однозначности (точки отрезков на одинаковом расстоянии от центра отрезка склеиваются):
на отрезке с центром в т.

:
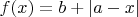
,
на отрезке с центром в т.

:

.
Здесь

и

.
-- 14.12.2017, 15:06 --Еще хотел уточнить по 1-й задаче. Я как будто нашел недочет в своем доказательстве:
Пусть

по определению 2.
Предположим, что определение 3 не выполнено, т.е.

такой, что

.
Возьмем произвольное

и возьмем

такой, что

. Далее, на каждом (

-м) шаге уменьшаем

вдвое и берем
 такой, что
такой, что 
. Получим последовательность

, для которой последовательность
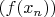
не сходится к

. Полученное противоречие доказывает, что из определения 2 следует определение 3.
К выделенному надо добавить: и такой, что

. Иначе в последовательности могут быть одинаковые иксы. Но потом я подумал, и понял что все иксы все равно не могут быть одинаковыми при стремлении

к нулю, а конечное число одинаковых ни на что не влияет, все равно будет

. Я прав, мое старое доказательство не нуждается в этом дополнении?