Здравствуйте, не разобрался в доказательстве Леммы:
Пусть

Если
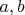
целые положительные числа, тогда для всех
![$x\in [0,1]$ $x\in [0,1]$](https://dxdy-04.korotkov.co.uk/f/b/2/2/b22db4945452a857d35a63a3f0ea506682.png)

Proof: Again, this proof can be done geometrically, noticing that each of the line segments that constitute the graph of

has as its image the interval [O, 1], so the graph of

will be replicated inside each of these corresponding intervals, as shown in FIGURE2.

На основании чего автор утверждает, что "т.к. каждый линейный сегмент графика, составляющих

, имеет в качестве своего образа, отрезок [0,1], график

будет повторён внутри каждого из соответствующих интервалов"? Конечно, можно влоб построить

и прийти к
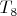
, но сформулировано же для общего случая?



