
Если доопределить знак нулём в нуле, тогда функция справа на
![$[-\pi, \pi]$ $[-\pi, \pi]$](https://dxdy-04.korotkov.co.uk/f/b/4/f/b4f4f90db968d4bd35772592503f5db782.png)
правильно передаёт сумму ряда. Фактически, один из рядов убился. Решение имеет вид довольно дикий. Мы исходим из двойного ряда

где

зависит от того, равно ли нулю

или нет. Оставим пока этот коэффициент на месте. Ряд внутри с помощью упомянутой формулы можно отсуммировать.
Здесь

и

. В силу положительности

и

для числа

верхняя грань равна

и нижняя грань равна

(не достигаются, так как

или

запрещено). Стало быть, формула выше применима, и

Со второй штукой всё несколько сложнее. Там

, нижняя грань - это нуль, а верхняя - это

, то есть в промежуток не совсем впишется. Но по отдельности на промежутке

всё ок,а промежуток

можно перевести в промежуток

вычитанием

. Рассмотрим преобразование

. В ряде изменится синус:

то есть ряд не изменится. В сумме ряда получаем

.
Итак, фиксируем

, делаем преобразование, получаем на


Справа функция, которая равна

в случае, если

. Ну вот и всё, мы описали полностью обе суммы, значит, внутренний ряд действительно сворачивается и остаётся один внешний.
-- 04.12.2017, 00:07 --В таком случае можно объединить в одну формулу вторую штуку:
 -- 04.12.2017, 00:13 --
-- 04.12.2017, 00:13 --Фух, управились. Что со сходимостью? Сходимость этих штук при

- вообще говоря экспоненциально быстрая. Но есть исключения.
1) Если у нас

и

, то для того ряда
у которого

, нужно подставлять

напрямую, так как сингулярности там нет. Второй ряд суммируется как обычно и сходится экспоненциально быстро. Коэффициент

здесь определяется нормировкой бесселей и оттуда вылезет

, но это неважно, так как экспонента одного из рядов его забьёт, а во второй подставляем чистый ноль. Всё сходится.
2) Если у нас

, то коэффициент

здесь порядка единицы и определяется только нормировкой синуса (то есть от
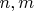
не зависит). Бессель при этом исчезает. Если

, то всё хорошо, и оба ряда сходятся по экспоненте, причём один из рядов (где

) сходится тем медленнее, чем ближе

. Подставлять

напрямую и получать ноль там нельзя из физического смысла, а пределы

дают константу и расходимость по

имеет вид

, то есть расходимость линейна по

.
Во всех остальных случаях всё ок.