Да, так. Теперь попробуйте доказать, что скажем если

и

, то
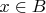
.
неудачно сформулированное подзадание. Ведь из

следует

в любом случае, условие

здесь не требуется.
Кроме того, Вы наверняка хотели написать в правой части

вместо

.
Надо было сформулировать подзадание как-нибудь так: если

, то

эквивалентно

(а не

!).
Я думаю, что из посылки нам известно, что любой

который принадлежит

, принадлежит и

. Так как пересечение множеств требует и то и другое, то я бы заменил (опустил)

на
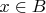
и получил просто
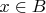
. Я не понимаю как это записывается.
Насчёт формы записи не беспокойтесь сильно: она не важна, если всё логично и обосновано.
Ну, конечно, если Вас интересует формализованная теория, то форма записи важна, а так вполне можно прожить, не думая о каком-то "правильном оформлении".
Так как Вас выше немного запутали (ненамеренно), расскажу как решать одно из подзаданий. С остальными разберётесь сами.
Итак, дано что

. Тогда



И



(в одну сторону);



(в силу

)


(в силу

и

) (в другую сторону).
Итак, мы доказали, что если

, то



. Эта эквивалентность означает, что

.
Тем самым, доказано, что из

следует

. Что там ещё осталось доказать?



