Задача 7.б.
Доказать, что

.
Доказательство.
Для установления зависимости между

и

сначала зададим

такое, что
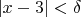
, и найдем

такой, что
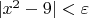
.
Используем следующие свойства модуля (взяты из Википедии):


По свойству (2),

и значит
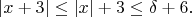
Далее, по свойству (1),
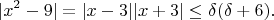
Таким образом, для произвольного положительного
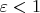
берем положительное
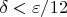
, тогда

, что означает что

выполнено
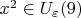
.
-- 23.11.2017, 16:52 --Перед задачей 13 хочу дополнить свое решение задачи 3, дав определение предела слева (справа) через предел последовательности (в стиле определения 2).
Пусть функция

определена на множестве

и точка

является предельной точкой множества

(

). Число

называется пределом слева (справа) функции

в точке

, если для любой последовательности

элементов множества

(

), сходящейся к

, последовательность
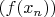
сходится к

.
Задача 13.
Функция, монотонная на интервале
![$]a,b[$ $]a,b[$](https://dxdy-04.korotkov.co.uk/f/b/8/8/b88dc426f03d472a567196e74f3a404782.png)
, имеет предел как слева, так и справа в каждой точке этого интервала.
Доказательство.
Пусть функция

монотонна на
![$]a,b[$ $]a,b[$](https://dxdy-04.korotkov.co.uk/f/b/8/8/b88dc426f03d472a567196e74f3a404782.png)
.
Возьмем произвольный
![$x_0\in]a,b[$ $x_0\in]a,b[$](https://dxdy-02.korotkov.co.uk/f/d/2/c/d2c3a8a7e695460718a5ae4a996dc80382.png)
.
Из любой последовательности

из чисел интервала
![$]a,x_0[$ $]a,x_0[$](https://dxdy-03.korotkov.co.uk/f/a/3/6/a36080e0daf388b9bbaefb5a6f0ce89b82.png)
можно выделить монотонно возрастающую подпоследовательность
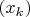
(задача 7 листка 12), которая также будет сходиться к

(задача 10 листка 11). Последовательность

является монотонной, т.к.

и
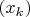
монотонны.

также является ограниченной, т.к. она ограничена числами

и

, где
![$x\in]a,x_0[$ $x\in]a,x_0[$](https://dxdy-03.korotkov.co.uk/f/2/4/b/24b74f561419ece8d67330a9e06744fc82.png)
, сверху и снизу (или наоборот - в зависимости от вида монотонности

). Следовательно,

сходится (задача 9 листка 12). Аналогично, для любой монотонно убывающей подпоследовательности

последовательности

из чисел интервала
![$]x_0,b[$ $]x_0,b[$](https://dxdy-01.korotkov.co.uk/f/4/f/f/4ff2e1de62abfb967e2a73b05dc9468b82.png)
последовательность

является монотонной (если

монотонно неубывающая, то

монотонно невозрастающая, и наоборот) и ограниченной, и следовательно, сходится.
-- 23.11.2017, 16:54 --Задача 14.
Дать определение функции, стремящейся к

при

, стремящемся к

.
Ответ.
Пусть функция

определена на множестве

и точка

является предельной точкой этого множества.
Определение через предел последовательности (в стиле определения 2).

стремится к

в точке

, если для любой последовательности

элементов множества

, сходящейся к

, последовательность
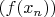
стремится к

.
Определение на языке

-

:

стремится к

в точке

, если

такое, что

выполняется условие

.
Обозначение:
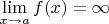
(или

при

).
-- 23.11.2017, 16:54 --Задача 15.
Пусть функция

не обращается в ноль в некоторой окрестности точки

. Доказать, что
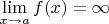
тогда и только тогда, когда

.
Доказательство следует из аналогичного утверждения для предела последовательности (задача 4 листка 12), примененного к последовательности значений

из определения 2.