числа вида x.99999 и (x+1).000

[vesely_gnom]

ребята подскажите плиз
числа вида напрмер 4.0000 и 3.9999(9) считаются равными.
а что если мы скажем что в конце второй записи есть конечное число восьмерок допустим?
будет ли оно отличаться от 4?
спасибр

[Xaositect]

У десятичной дроби 3.99999(9) нет конца, поясните, что Вы имеете в виду.

[vesely_gnom]

Xaositect в сообщении #1266235 писал(а):

У десятичной дроби 3.99999(9) нет конца, поясните, что Вы имеете в виду.

то есть я не могу так взять и сказать что у этого числа есть конец? а как соотноситмся множество нарисованных девяточек и того что нельзя нарисовать?

-- 18.11.2017, 00:35 --

и кстати есть числа вида ......999 например? чем они отличаются друг от друга?

[mihaild]

vesely_gnom в сообщении #1266240 писал(а):

а как соотноситмся множество нарисованных девяточек и того что нельзя нарисовать?

А что это вообще значит?
Есть некоторое вещественное число. Его можно обозначать как $4$, $4.000\ldots$, $3.999\ldots$, $2+2$ и т.д. Или же можно сказать, что под $3.999\ldots$ понимается предел последовательности $3, 3.9, 3.99, \ldots$ - можно доказать, что этот предел существует и равен $4$.

vesely_gnom в сообщении #1266240 писал(а):

и кстати есть числа вида ......999 например?

Нет. Если хотите, можете попробовать как-нибудь определить, но общепринятого смысла у этой записи нет.

[vesely_gnom]

mihaild в сообщении #1266245 писал(а):

vesely_gnom в сообщении #1266240 писал(а):

а как соотноситмся множество нарисованных девяточек и того что нельзя нарисовать?

А что это вообще значит?
Есть некоторое вещественное число. Его можно обозначать как $4$, $4.000\ldots$, $3.999\ldots$, $2+2$ и т.д. Или же можно сказать, что под $3.999\ldots$ понимается предел последовательности $3, 3.9, 3.99, \ldots$ - можно доказать, что этот предел существует и равен $4$.
прелел существует так как для сколь угодно малого x найдется n такое что 4 — у(n) < x? но что бы это доказать мы должны построить эти x и у

vesely_gnom в сообщении #1266240 писал(а):

и кстати есть числа вида ......999 например?

Нет. Если хотите, можете попробовать как-нибудь определить, но общепринятого смысла у этой записи нет.

а допустим числа вида 8a8b8c... где a, b,c... счетные множества? ну и число восьмерок допустим может быть счетным? а насчет ...999. тамнет отношений упорядоченности например

[mihaild]

vesely_gnom в сообщении #1266254 писал(а):

а допустим числа вида 8a8b8c... где a, b,c... счетные множества?

Что это такое? В десятичной дроби до запятой может быть только конечное число цифр (запись целой части).

vesely_gnom в сообщении #1266254 писал(а):

тамнет отношений упорядоченности например

Я не знаю, что такое "отношения упорядоченности", не понимаю, где "там" и соответственно не понимаю, о чем вы.

[arseniiv]

vesely_gnom в сообщении #1266254 писал(а):

а допустим числа вида 8a8b8c... где a, b,c... счетные множества?

Цифры дробной части десятичной записи образуют последовательность, т. е. это отображение из множества $\mathbb N$ натуральных чисел в множество $\{0,\ldots,9\}$. Ваша «последовательность» не будет последовательностью (потому что это отображение не из $\mathbb N$), вот и всё. По определению десятичная запись $0{,}a_1a_2\ldots$ означает сумму ряда $\sum_{i=1}^\infty 10^{-i}a_i$, для вашей (я её исправлю) записи $0{,}8a_1a_2\ldots8b_1b_2\ldots8c_1c_2\ldots$ ничего подобного определить не получится.

[vesely_gnom]

mihaild в сообщении #1266258 писал(а):

vesely_gnom в сообщении #1266254 писал(а):

а допустим числа вида 8a8b8c... где a, b,c... счетные множества?

Что это такое? В десятичной дроби до запятой может быть только конечное число цифр (запись целой части).

а если это трансцентентное число? или иррациональное? то о чем вы говорите можно отнести к рациональным дробям разве нет? у них вроде конечное число цифр в записи

vesely_gnom в сообщении #1266254 писал(а):

тамнет отношений упорядоченности например

Я не знаю, что такое "отношения упорядоченности", не понимаю, где "там" и соответственно не понимаю, о чем вы.
там это в дррбях вида мммм надо строже определить? пооучается дробь вида 0.000(счетное множество нулей)999 но тут множество нулей бесконечное поэтому это не совсем число так?

-- 18.11.2017, 01:22 --

arseniiv в сообщении #1266260 писал(а):

vesely_gnom в сообщении #1266254 писал(а):

а допустим числа вида 8a8b8c... где a, b,c... счетные множества?

Цифры дробной части десятичной записи образуют последовательность, т. е. это отображение из множества $\mathbb N$ натуральных чисел в множество $\{0,\ldots,9\}$. Ваша «последовательность» не будет последовательностью (потому что это отображение не из $\mathbb N$), вот и всё. По определению десятичная запись $0{,}a_1a_2\ldots$ означает сумму ряда $\sum_{i=1}^\infty 10^{-i}a_i$, для вашей (я её исправлю) записи $0{,}8a_1a_2\ldots8b_1b_2\ldots8c_1c_2\ldots$ ничего подобного определить не получится.

хммм а не будет ли это изоморфно 3 числам? или нам для этого нужно найти вторую и третью восьмерки и как только мы это сделаем(зафиксируем)

[DeBill]

vesely_gnom в сообщении #1266240 писал(а):

есть числа вида ......999

Вообще то есть. Это - $p$-адические числа. Вот только это не числа....

(Оффтоп)

Нда. Это я к той каше, что, видимо, имеется в голове у ТС по числам, добавил свою толику масла...

[arseniiv]

DeBill, спасибо.

vesely_gnom в сообщении #1266264 писал(а):

хммм а не будет ли это изоморфно 3 числам?

Давайте вы не будете пользоваться терминами, значение которых от вас малость ускользает, а то это смахивает на троллинг.

[vesely_gnom]

arseniiv в сообщении #1266274 писал(а):

DeBill, спасибо.

vesely_gnom в сообщении #1266264 писал(а):

хммм а не будет ли это изоморфно 3 числам?

Давайте вы не будете пользоваться терминами, значение которых от вас малость ускользает, а то это смахивает на троллинг.

ладно) я не тролль обычный программист с математическим образованием))) просто стало интересно прчему так... ну ок это не отображение из N а из чего тогда? $3N$?

-- 18.11.2017, 01:37 --

DeBill в сообщении #1266270 писал(а):

vesely_gnom в сообщении #1266240 писал(а):

есть числа вида ......999

Вообще то есть. Это - $p$-адические числа. Вот только это не числа....

(Оффтоп)

Нда. Это я к той каше, что, видимо, имеется в голове у ТС по числам, добавил свою толику масла...

пытаться разобраться лучше чем не пытаться)) а где можно почитать про них? желательно для чайноков? я знаю что это типа расширение действительных чисел, а подробнее нет.ъ

[arseniiv]

vesely_gnom в сообщении #1266277 писал(а):

ну ок это не отображение из N а из чего тогда? $3N$?

Тут важно рассматривать, как можно догадаться, не просто множества, а множества вместе с порядком на них, и отображения, сохраняющие порядок. В таком случае вместо $(\mathbb N,<_{\mathbb N})$ обычно пишут $\omega$. Для порядков можно ввести операцию сложения: $(A,<_A)+(B,<_B)$ будет означать множество $A\sqcup B$ с порядком на нём таким, чтобы все элементы вложения $A$ в $A\sqcup B$ были меньше любого элемента вложения $B$, а на сами вложения $A, B$ переносились порядки $<_A$ и $<_B$. 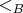В вашем случае будет отображение из $\omega+\omega+\omega$. Конечно, носитель этого порядка тоже счётный, но отображений между им и $\omega$, сохраняющих порядок, нет. А суммировать мы можем только ряд, члены которого образуют последовательность (коряво написано, ну да ладно). Так что никакого правильного способа сопоставить вашим штукам вещественные числа будет нельзя. Что-то другое — возможно, но тут надо иметь в виду, что всевозможных обобщений вещественных чисел уже придумано много, и вряд ли это даст что-то доселе неизведанное и интересное.

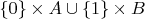
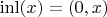
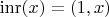
(Вероятно, придётся ещё добавить, что $A\sqcup B$ — дизъюнктное объединение множеств, которое можно определить как $\{0\}\times A\cup \{1\}\times B$ — каждый его элемент «помнит», из левого или из правого операнда был «взят». Функции $\mathrm{inl}\colon A\to A\sqcup B$, $\mathrm{inr}\colon B\to A\sqcup B$, $\mathrm{inl}(x) = (0,x)$, $\mathrm{inr}(x) = (1,x)$ зовутся каноническими вложениями, и сами их образы тоже можно звать вложениями ($A$ или $B$ в $A\sqcup B$), что и упоминается выше.)

[Someone]

vesely_gnom в сообщении #1266277 писал(а):

я … обычный программист с математическим образованием

С математическим??? Неужели уже так стали математиков-программистов учить?

vesely_gnom в сообщении #1266277 писал(а):

я знаю что это типа расширение действительных чисел

Ни в коем случае. Расширение поля рациональных чисел — да. Поле действительных чисел тоже является расширением поля рациональных чисел.

vesely_gnom в сообщении #1266277 писал(а):

а где можно почитать про них?

Вас в поисковых системах заблокировали?

А если по простому — это "числа", записи которых бесконечны влево (а вправо конечны, то есть, после запятой может быть только конечное количество цифр). Сложение и умножение выполняются как обычно. Если основание системы счисления — простое число $p$ (или степень простого числа $p$), то получается поле $p$-адических чисел, а если составное (точнее, имеет не менее двух различных простых делителей), то получается кольцо с делителями нуля. Только не надо называть $p$-адические числа "бесконечными". Они не больше бесконечные, чем действительные числа. Например, $10$-адическое число $\ldots 66667$ — это $\frac 13$, потому что $\ldots 66667\times 3=\ldots 00001=1$. А $\ldots 99999$ — это $-1$ (знак "$-$" при записи $p$-адических чисел не нужен).

[vesely_gnom]

Someone в сообщении #1266327 писал(а):

vesely_gnom в сообщении #1266277 писал(а):

я … обычный программист с математическим образованием

С математическим??? Неужели уже так стали математиков-программистов учить?

vesely_gnom в сообщении #1266277 писал(а):

я знаю что это типа расширение действительных чисел

Ни в коем случае. Расширение поля рациональных чисел — да. Поле действительных чисел тоже является расширением поля рациональных чисел.

vesely_gnom в сообщении #1266277 писал(а):

а где можно почитать про них?

Вас в поисковых системах заблокировали?

А если по простому — это "числа", записи которых бесконечны влево (а вправо конечны, то есть, после запятой может быть только конечное количество цифр). Сложение и умножение выполняются как обычно. Если основание системы счисления — простое число $p$ (или степень простого числа $p$), то получается поле $p$-адических чисел, а если составное (точнее, имеет не менее двух различных простых делителей), то получается кольцо с делителями нуля. Только не надо называть $p$-адические числа "бесконечными". Они не больше бесконечные, чем действительные числа. Например, $10$-адическое число $\ldots 66667$ — это $\frac 13$, потому что $\ldots 66667\times 3=\ldots 00001=1$. А $\ldots 99999$ — это $-1$ (знак "$-$" при записи $p$-адических чисел не нужен).

многое забыл...

[Lia]

vesely_gnom
Замечание за избыточное цитирование. Используйте кнопку "Вставка" после выделения нужного фрагмента текста.