Продолжаю прорешивать задачи из книжки Давидовича и ко
http://www.mccme.ru/free-books/57/davidovich.pdf.
В этой теме - листок 15, делаю его параллельно с
предыдущим.
Прошу уважаемых форумчан проверить мои доказательства, как и в моих предыдущих темах. Помимо всего прочего, буду благодарен за замечания по стилистике доказательств.
Определение 1.
Множество

называется проколотой

-окрестностью точки

.
Определение 2.
Пусть функция

определена на множестве

и точка

является предельной точкой этого множества. Число

называется пределом функции

в точке

, если для любой последовательности

элементов множества

, сходящейся к

, последовательность
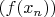
сходится к

. Обозначение:

(или
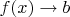
при

).
Определение 3.
Пусть функция

определена на множестве

и точка

является предельной точкой этого множества. Число

называется пределом функции

в точке

, если

такое, что

выполняется условие
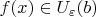
.
Задача 1.
Доказать равносильность определений 2 и 3.
Уже долго бьюсь с этим доказательством, ощущение что хожу вокруг да около, и все чего-то не хватает. Прошу помощи.
Мои мысли следующие.
Из условий обоих определений (из предельности

) следует существование сходящейся к

последовательности из элементов множества

, т.е.
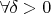
внутри
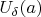
содержится бесконечно много элементов

.
Из обоих определений следует, что последовательность значений функции

, сходящаяся к

, существует.
Теперь определения с доп. комментариями.
Определение 2: ... для любой последовательности

элементов множества

, сходящейся к

(а такая последовательность существует), последовательность
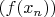
сходится к

(и последовательность
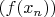
обязательно существует, раз существует

). В этом определении для любого

существует

..., т.е. имеем зависимость

, причем делая

сколь угодно малым, соответствующий

тоже сколь угодно близко приближается к нулю.
Определение 3: ...

такое, что

(а таких

существует бесконечно много, и из них можно составить последовательность, сходящуюся к

) выполняется условие
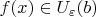
. Приближая

сколь угодно близко к нулю, получим сходящуюся к

последовательность значений

, при этом соответствующая последовательность аргументов будет содержаться внутри соответствующей
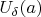
. В этом определении для любого

существует

..., т.е. имеем зависимость

, но неочевидно что с уменьшением

уменьшается и

.