deep downспасибо за доп.вопрос, обязательно разберусь с этим. Сейчас хочу заранее прояснить вопрос по следующей - неграфической - задаче.
Сначала определения.
Определение 4.
Множество

называется симметричным (относительно нуля), если для любого

верно, что и

.
Определение 5.
Функция

называется четной (нечетной), если множество

симметрично и для всякого

выполняется условие

(

).
А вот непонятная задача.
Задача 3.
Доказать, что график четной (нечетной) функции симметричен относительно оси

(начала координат).
Я не понимаю, что тут подразумевается под симметричностью графика. Вот определение графика функции из листка 3 "Отображения множеств":
Графиком отображения

называется множество

, состоящее из всех пар вида

.
По определению 4 выше, график

симметричен (относительно начала координат?), если для любого

верно, что и

.
Пусть

. Что в таком случае

?

? Чтобы определить противоположный элемент, надо ведь ввести сложение на этом множестве, верно? Что-то типа

?
Или симметричность тут подразумевается на интуитивном уровне:

и
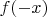
равноудалены от

и имеют одинаковый знак для любого

(для четной функции)? Другими словами,

. В таком случае "доказательство" есть просто определение четной и нечетной функции.