Draeden писал(а):
Разве это так очевидно ?
Даже если многочлен вещественный, то прикинуть "на глаз" местоположение его экстремумов довольно непросто. В данном случае многочлен комплексный, и я не представляю, где его производная обращается в ноль. Хотя может быть я не вижу очевидного...
А я и не говорю, что это очевидно. Зато в одном из предыдущих сообщений я Вам с полной очевидностью показал, что задача отыскания нулей функции
 равносильна
равносильна задаче отыскания нулей у производной многочлена, имеющего корни

.
Профессор Снэйп писал(а):
Угу. Тут если ввести многочлен

то

(штрих, как обычно, обозначает производную). Получается, что надо искать нули многочлена

.
А с чего Вы, собственно, взяли, что Ваша задача должна иметь простое решение?
Добавлено спустя 6 минут 45 секунд:
Но, кстати, насчёт "примерного" отыскания нулей производной.
Если многочлен вещественный (и все корни кратности 1), то понятно, где "примерно" располагаются нули производной: между корнями исходного многочлена. К какому корня что ближе --- уже более сложный вопрос, но и он решается путём некоторого анализа взаимного расположения корней.
К примеру, пусть многочлен

. Корень производной
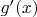
, лежащий между

и

к чему ближе: к единице или к тройке? А?

Ну а если корни комплексные... невелика разница на самом деле.



