ewert (и остальные), как Вы считаете, можно ли пропустить оставшиеся в этом листке задачи, начиная с 17й, без ущерба для дальнейшего понимания? Я чувствую что уже достаточно времени потратил на предел последовательности, и пора двигаться дальше. Я сделал еще задачи 14-16, по-моему они довольно важны (возможно я ошибаюсь): 14я о том что показательная функция растет быстрее степенной, результат 15й наверняка будет постоянно всплывать дальше, 16я - это что-то из теорвера/статистики. Оставшиеся задачки как-то не кажутся интересными. Короче, сейчас выложу еще 14-16, исправлю все замечания в этой теме, и перейду к следующему листку. Норм, как считаете?
-- 27.06.2017, 19:04 --Задача 14*.
Найти

(
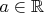
,

).
Решение.
При

предел очевидно равен нулю.
Предположим теперь, что

. Тогда
![$\sqrt[k]{a}>1$ $\sqrt[k]{a}>1$](https://dxdy-01.korotkov.co.uk/f/0/4/7/04787161918fdcc7ebc0c2455c47cafe82.png)
. Обозначим
![$\sqrt[k]{a}=1+\varepsilon$ $\sqrt[k]{a}=1+\varepsilon$](https://dxdy-01.korotkov.co.uk/f/8/7/b/87b8c0374342a2d7fda9e1bf1d85065282.png)
. Разложение по формуле бинома Ньютона

содержит положительные слагаемые со старшими степенями

более

(конкретней, от нулевой степени

в

до

-й степени в

), следовательно

. Отсюда

.
Из

следует

, значит при

последовательность стремится к бесконечности.
-- 27.06.2017, 19:05 --Задача 15*.
Доказать, что
![$\lim\limits_{n\to\infty}\sqrt[n]{n}=1$ $\lim\limits_{n\to\infty}\sqrt[n]{n}=1$](https://dxdy-03.korotkov.co.uk/f/6/7/0/670bb5043cee34c4ff6511cc9636c46d82.png)
.
Доказательство.
Сперва отметим, что

выполнено

Правая часть неравенства очевидна (т.к.

), а левая доказывается разложением по формуле бинома Ньютона, аналогично задаче 14.
Отсюда
![$$
1-\varepsilon<\sqrt[n]{n}<1+\varepsilon.
$$ $$
1-\varepsilon<\sqrt[n]{n}<1+\varepsilon.
$$](https://dxdy-04.korotkov.co.uk/f/b/3/9/b39501883ef5e566de9e3ee679eff1a882.png)
Пусть теперь

-- б.м.в. с положительными членами. Тогда
![$$
1-\alpha_n<\sqrt[n]{n}<1+\alpha_n,
$$ $$
1-\alpha_n<\sqrt[n]{n}<1+\alpha_n,
$$](https://dxdy-02.korotkov.co.uk/f/d/e/7/de7db614fa280925c23b40ece948c2ae82.png)
откуда согласно принципу двух милиционеров следует стремление
![$\sqrt[n]{n}$ $\sqrt[n]{n}$](https://dxdy-01.korotkov.co.uk/f/8/b/b/8bb34ec8fe5843ea6852d20edd9260ad82.png)
к единице.
-- 27.06.2017, 19:14 --Задача 16*.
Доказать, что если последовательность

сходится, то последовательность средних арифметических

также сходится и

.
Доказательство.
Пусть

при

. Тогда

, где

-- б.м.в., и

Возьмем произвольный

и

такое что


. Обозначим

. Тогда


, и значит

Отсюда

.



