Пусть

,

.

, значит по задаче 4

.
Наверное не надо было тут никакого

вводить, а надо было просто написать:



, значит по задаче 4

.
-- 03.06.2017, 13:37 --10.б)

(

)
Вот с этим пришлось помучиться, хотя в итоге не так уж сложно оказалось.
Доказательство сходимости.
Заметим, что

выполнено

, т.е. все члены

начиная с некоторого номера убывают. Значит, среди всех членов

найдется наибольший. При этом множество всех членов

ограничено снизу нулем. Значит

ограничена.
Выделим все члены с номером

в монотонно убывающую подпоследовательность
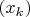
. Из ограниченности и монотонности
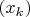
следует ее сходимость (задача 9).

отличается от
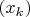
дополнительным наличием не более чем конечного числа членов, которые не могут повлиять на наличие/отсутствие у

предельных точек по сравнению с
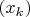
. Следовательно, предел
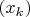
также является пределом

.
Найдем предел.
Предположим,

.
Тогда

согласно п.а).

, т.к.

для любого

.
Следовательно,

Пусть теперь

.
Обозначим

,

. Для любого

выполнено

, где

. Согласно п.а),

, а значит и

при

. Отсюда

.
-- 03.06.2017, 13:41 --10.в)

,

Доказательство сходимости.
Покажем что каждый

(по индукции). База:

. Переход: пусть

, тогда

. Таким образом мы сразу получили ограниченность и монотонность

, из которых следует ее сходимость (задача 9).
Пока не могу понять, как здесь найти предел, а точнее доказать что он равен нулю. Конечно, можно было бы выписать явную формулу для

подключив теорию рекуррентных соотношений, но "мы этого еще не проходили", и тут видимо предполагается какой-то другой подход.