Лучше пойти в каталог книг по физике
и выбрать намного более современный учебник.
Вы считаете, что Эйнштейн устарел?
Думаю Вам должен нравится Фейнман и его лекции. Это нормально. Мне, кроме, того нравится Эйнштейн, Зоммерфельд, С. Вавилов и многие из почивших и ныне здравствующих. Стиль работ Эйнштейна великолепен. Я знаю человека, автора нескольких монографий и учебников, который учился писать по работам Эйнштейна, хотя его специальность ФТТ.
И еще одно качества Эйнштейна, которое не достает порой нынешним. Он постоянно сомневался, не боялся признать свои ошибки.
Цитата:
MOPO3OB, предупреждение за использование бессодержательных аргументов и тезисов, игнорирование аргументов или содержательных вопросов собеседников, формальные отписки, не касающиеся сути дела.
Как только я увижу содержательные вопросы относящиеся к статье, я непременно на них отвечу, если найду время разумеется.
|
! |
GAA: |
| Пожалуйста, обсуждайте предупреждения модератора в ЛС или в разделе «Работа форума». Блокировка на две недели. |
Цитата:
Замечательно. Значит, метрика (2) - это просто метрика плоского пространства Минковского в координатах Меллера
Я рад, что Вы немного разобрались. Хотя могли бы просто перейти к содержательной части статьи.
Цитата:
Посчитайте аккуратнее: даже тензор Римана для этой метрики должен получиться нулевым.
Спасибо, я в курсе. Вот цитата из новой
статьиЦитата:
О трудности описания систем ускоренных тел говорит, что только в 1943 году К. Мёллеру [2, 3] удалось корректно описать неинерциальною систему отсчета с помощью общей теории относительности. Метрика системы отсчета Мёллера плоская, причем единственная плоская из метрик вида

. Это утверждение легко доказывается, поскольку единственное нетривиальное решение дифференциального уравнения
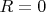
– метрика Мёллера с

, здесь α_x – компонента ускорения, в согласии с (1). Однако метрика Мёллера описывает однородное поле ускорений только в первом приближении.
Я постараюсь ответить на вопросы по существу. Только не надо давить на меня и демонстрировать эрудицию a la Мунин.



