Пример неэффективного доказательства в ZF. Мы можем доказать, что любое множество можно вполне упорядочить.
В ZF не можем. В ZFC можем.
За примером неконструктивности не надо далеко ходить. Если мы в доказательстве говорим "возьмём любое

", не указывая никакого конкретного

, то наше доказательство заведомо не конструктивно. Но мы можем сказать "пусть

", тогда в этом месте наше рассуждение будет конструктивным.
Не ZF(C) сформулирована, а модель построена в X; ZF(C) формулируется чисто синтаксически, независимо от семантики.
Вы не правы. Для формулировки формальной теории нужна метатеория. В этой метатеории определяются алфавит, термы, формулы, задаются аксиомы, определяется понятие доказательства и доказываются метатеоремы (например, о доказуемости или недоказуемости какой-нибудь формулы). Кроме того, в ней же можно строить модели формальной теории. В каких-то случаях может потребоваться мета-метатеория. В качестве метатеории чаще всего используется естественный язык, но при нужде можно взять и какую-нибудь формализованную теорию.
метамножество всех множеств ZFC не является множеством всех множеств в самой ZFC, даже если вследствие какой-то причуды модели оно принадлежит этой модели. Один и тот же объект в ZFC и в X может играть совершенно разную роль.
Я несколько разовью этот тезис, показав пример, когда отношение

в метатеории не совпадает с отношением

в построенной с её помощью модели.
В качестве метатеории X мы возьмём ZFC. В ней натуральный ряд (с нулём; кто не хочет считать ноль натуральным числом, может называть это множество первым бесконечным ординалом) определяется как наименьшее индуктивное множество. Аксиомы Пеано для этого множества являются теоремами ZFC. В этой модели натуральные числа являются множествами:

,

,

,

,

,…; следующие натуральные числа определяются индуктивно формулой

. Мы не будем рассматривать эту арифметику как отдельную теорию, будем считать её просто частью метатеории X, язык которой пополнен символами для арифметических операций и соответствующими правилами для образования арифметических формул.
Теперь, используя натуральные числа, мы построим модель теории наследственно конечных множеств, которая есть ZFC, в которой аксиома бесконечности заменена её отрицанием. Элементы этой модели являются определёнными выше натуральными числами. Связь между числами и изображаемыми ими множествами определяем так:
1)

;
2) если

,

,
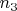
,…,

попарно различны, то

.
Тогда

,

,

,

,

,…
Сравнивая написанные равенства в метатеории X и в теории наследственно конечных множеств, видим, что, например, в первом случае символ

обозначает множество с двумя элементами

и

, а во втором — множество с одним элементом

, хотя с точки зрения метатеории

— один и тот же объект в обоих случаях. По-хорошему, во второй теории следовало бы использовать другие символы для обозначения отношения принадлежности и для образования множеств.
Примечание. Теория наследственно конечных множеств встречается в книге П. Дж. Коэна "Теория множеств и континуум-гипотеза" (глава I, § 6, теория

), где утверждается, что эта теория эквивалентна арифметике Пеано. Я не знаю, доказуема ли схема аксиом индукции в ZFC с отрицанием аксиомы бесконечности, но Коэн формулирует эту схему в явном виде.
-- Сб май 13, 2017 01:47:41 --Нашёл
статью, где этот вопрос проясняется. Действительно нужна дополнительная аксиома.



