Летающий волчок

[amon]

О заряженном кольце. Вот рассчитанный потенциал кольца и гравитации. Формулы будут позднее, сейчас набивать некогда. Задача, к счастью, аксиально симметричная, поэтому все можно нарисовать. Ось $x$ это радиус, $z$ это высота (цилиндрические координаты), от угла ничего не зависит. Итак, общий вид потенциала.

Вложение:

RimgPotentialWhole.gif [ 17.36 Кб | Просмотров: 2902 ]

Казалось бы, вот она, победа Лапласиан, но если знать куда смотреть, то...

Вложение:

RingPotentialWell.gif [ 14.53 Кб | Просмотров: 0 ]

Расчетные формулы (на предмет проверки не соврал ли я где по обыкновению) и толкования чуть позже. Толкования у меня два - одно, что только так и должно быть, а второе - что так не бывает. Какое правильное - пока не решил. Оставляю интригу до вечера


19.03.2017
Для археологов: картинка ошибочная, правильное толкование - второе.

[fred1996]

Математически гравитационный потенциал и потенциал пружинки дают весьма похожий результат.
Замкнутые орбиты у них эллипсы.
Только для гравитационного потенциала центр гравитации находится в одном из фокусов эллипса, а в случае пружинки в центре.

-- 16.03.2017, 08:28 --
Для кольца имеем следующее:
В цилиндрических координатах лапласиан выглядит так:

$\Delta U=\frac{1}{r}\frac{\partial}{\partial r}(\frac{1}{r}\frac{\partial U}{\partial r}) + \frac{\partial^2 U}{\partial z^2} + \frac{1}{r^2}\frac{\partial^2 U}{\partial \varphi^2} = 0$

Поскольку у нас задача симметрична относительно углового поворота и мы выбрали точку локального экстремума, то уравнение упрощается:

$\frac{\partial^2 U}{\partial r^2} + \frac{\partial^2 U}{\partial z^2} = 0$

И если мы нашли минимум по оси $z$, то это автоматически будет максимумом по радиальному направлению $r$

[Munin]

amon
Я нашёл, где у вас ошибка! Вы Ring через m написали!

[Dmitriy40]

fred1996 в сообщении #1200962 писал(а):

И если мы нашли минимум по оси $z$, то это автоматически будет максимумом по радиальному направлению $r$

Вполне возможно, фотки и опыты с кольцевыми магнитами на стержне подтверждают. Тогда тот пенопластовый треугольник с магнитами на фото висит не точно над центрами больших магнитов, а немного с внутренней стороны каждого, так? Чтобы каждый большой магнит сталкивал его от себя, но в центр образующего треугольника. Хотя непонятно что мешает пенопластовому треугольнику провернуться вокруг вертикали и удалить все маленькие магниты от больших?

[fred1996]

Dmitriy40 в сообщении #1200995 писал(а):

fred1996 в сообщении #1200962 писал(а):

И если мы нашли минимум по оси $z$, то это автоматически будет максимумом по радиальному направлению $r$

Вполне возможно, фотки и опыты с кольцевыми магнитами на стержне подтверждают. Тогда тот пенопластовый треугольник с магнитами на фото висит не точно над центрами больших магнитов, а немного с внутренней стороны каждого, так? Чтобы каждый большой магнит сталкивал его от себя, но в центр образующего треугольника. Хотя непонятно что мешает пенопластовому треугольнику провернуться вокруг вертикали и удалить все маленькие магниты от больших?

Я думаю обычная инерция.
Для таких Инерционных треугольников возможно найти такое положеное неустойчивого равновесия, когда уход от этого равновесия займет существенное время. То есть неустойчивость получается не в радиальном направлении, а по поворотам.
Фактически конструкция треугольника имеет шесть степеней свободы и при хорошем юстировании можно добиться устойчивого ракновесия по пяти из них, исключая поворот вокруг вертикальной оси. А этот поворот достаточно инерционен.

[amon]

Ну вот. Формулы. Мы хотим сосчитать поле над кольцом в области, ограниченной радиусом кольца. Для этого надо решить простую школьную геометрическую задачку. Чертежик представлен на рисунке в свойственной мне изящной художественной манере. Если кто что поймет - буду очень благодарен

Вложение:

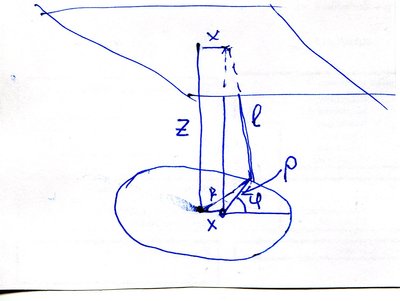ring.jpg [ 143.6 Кб | Просмотров: 0 ]

Задача - найти $l(x,\varphi).$ Из простой геометрии следует, что

$$ \begin{align} R^2&=x^2+\rho^2-2x\pho\cos\varphi\\ \rho&=x\cos\varphi+\sqrt{R^2-x^2\sin^2\varphi}\\ l^2&=z^2+\rho^2 \end{align} $$

Ну, вот, собственно, и золотой ключик:

$$ l^2(x,\varphi)=z^2+R^2+x^2\cos 2\varphi+2x\sqrt{R^2-x^2\sin^2\varphi} $$

Тогда наш злосчастный потенциал будет

$$ V(x,z)=\int\limits_{0}^{2\pi}\frac{d\varphi}{l}+\alpha z $$

Из соображений простоты взято $R=1,$ а из соображений наличия минимума вдоль $Z$ взято $\alpha=1.5$ и всё это хозяйство построено численно. Сразу отмечу, что поскольку $l(0,\varphi)$ от $\varphi$ вообще не зависит, то все производные берутся аналитически, но это слабо помогает. Дело в том, что квадратичная форма вторых производных оказывается вырожденной (как видно из вышеприведенных рисунков, дно ямки по $x$ очень плоское, что выражается в том, что почти все вторые производные зануляются).
Ну, вот, пока все. Проверяйте, а то может и обсуждать нечего.

(Оффтоп)

Munin в сообщении #1200982 писал(а):

Я нашёл, где у вас ошибка! Вы Ring через m написали!

Пошел искать пепел.

[Dan B-Yallay]

amon
Если я правильно помню физику, при смещении пробного заряда с линии оси $Оz$ в какую-нибудь сторону, распределение электрического заряда на кольце изменится и перестанет быть центрально-симметричным. Вы это учитывали или как? Я не вижу, но может где-то в формуле воткнуто, а я туплю...
Или считаем кольцо заряженным диэлекриком?

[amon]

Dan B-Yallay в сообщении #1201025 писал(а):

при смещении пробного заряда с линии оси $Оz$ в какую-нибудь сторону, распределение электрического заряда на кольце изменится

Это - чистая правда для металлического кольца, но ни что не мешает нам считать его диэлектрическим (задан не потенциал, а распределение заряда). Я считал для заданного распределения заряда (равномерного с единичной плотностью).

[Dan B-Yallay]

Ясно. Я пытаюсь рассмотреть шестиугольник и если не проврался, то там "ямка", но надо проверять. Тем более, что Лаплас запрещаэ и нэгодуэ...

PS. Что интересно: и для треугольника, и для шестиугольника и для кольца - максимум кулоновских сил на оси $Oz$ достигается в той же хитрой точке: $\Big(0,0,\dfrac 1{\sqrt{2}}\Big)$.
Она, эта точка, - она еще в плоском случае вылезла.

By the way: The electrostatic potential of a uniformly charged ring

[fred1996]

Dan B-Yallay в сообщении #1201029 писал(а):

Ясно. Я пытаюсь рассмотреть шестиугольник и если не проврался, то там "ямка", но надо проверять. Тем более, что Лаплас запрещаэ и нэгодуэ...

PS. Что интересно: и для треугольника, и для шестиугольника и для кольца - максимум кулоновских сил на оси $Oz$ достигается в той же хитрой точке: $\Big(0,0,\dfrac 1{\sqrt{2}}\Big)$.
Она, эта точка, - она еще в плоском случае вылезла.

By the way: The electrostatic potential of a uniformly charged ring

А тут как раз ничего удивительного.
Для $2N$ угольника максимум достигается для каждой пары симметричных точек. Поэтому и результат один. А вот для нечетного числа зарядов формула будет посложнее. Хотя в пределе для кольца опять получим ту же формулу.

[Dan B-Yallay]

Нашел вот такой разбор на сайте Alfred State Coll, NY.
Показывают вполне явную "ямку" у кольца:


Потенциал кольца в разрезе через центр:


-- Чт мар 16, 2017 14:16:20 --

fred1996 в сообщении #1201036 писал(а):

Для $2N$ угольника максимум достигается для каждой пары симметричных точек. Поэтому и результат один.

Вполне резонно, согласен.

[fred1996]

Dan B-Yallay
Это у вас показаны не ямки потенциала, а эквипотенциальные поверхности и совсем не в точках равновесия.
В случае точки равновесия Локально это будет двунаправленный конус.
И решение достаточно тривиально. Поскольку тангенс угла этого конуса определяется отношением вторых производных. А из Лапласа это единица. То есть эквипотенциальная поверхность будет коническая поверхность с углом раскрытия 90 градусов при вершине.

[Dmitriy40]

Я попробовал нарисовать поле векторов для горизонтальных сечений над плоскостью треугольника с одинаковыми зарядами в вершинах, посмотреть куда направлены силы в горизонтальной плоскости, после медитации "а что же я таки получил" выходит что хоть кое-где сила и направлена внутрь треугольника, но устойчивого равновесия нет. Похоже там стыкуются три седловидные поверхности с горбами примерно над зарядами, которые при удалении сечения вверх поднимают своё "дно" вплоть до получения выпуклого купола. Но даже до этого, выраженной ямки нет нигде, проекции векторов не зацикливаются, из любой точки существует путь вдоль векторов наружу, за границу области. Ну или я пропустил ямку при задании сечений по высоте.
Вот для кольца эти "долины" между зарядами наверное повышаются до уровня горбов над зарядами и получается сплошная стенка с ямкой в центре. Вероятно её же можно получить и для достаточно большого количества зарядов в вершинах многоугольника.

[Dan B-Yallay]

fred1996 в сообщении #1201041 писал(а):

Это у вас показаны не ямки потенциала, а эквипотенциальные поверхности и совсем не в точках равновесия.

Если я правильно понимаю, то речь идёт об этом:

Вот у нас эквипотенциальная поверхность. Поместим на дно центральной "лунки" пробный заряд такой массы, чтобы кулоновские силы отталкивания компенсировали силы тяжести. В каком направлении может двигаться пробный заряд, чтобы его потенциальная энергия не увеличивалась?

-- Чт мар 16, 2017 14:54:33 --

Dmitriy40

Dmitriy40 писал(а):

Похоже там стыкуются три седловидные поверхности с горбами примерно над зарядами, которые при удалении сечения вверх поднимают своё "дно" вплоть до получения выпуклого купола.

Я попробовал нарисовать проекцию кулоновских сил на вертикальную ось для шестиугольника. Если не проврался, вот что получилось:

Вложение:

Hex2.jpg [ 64.19 Кб | Просмотров: 0 ]

На мой взгляд дно лунки находися ниже, нежели седловые точки между зарядами.

[amon]

Dan B-Yallay в сообщении #1201051 писал(а):

Поместим на дно центральной "лунки" пробный заряд такой массы, чтобы кулоновские силы отталкивания компенсировали силы тяжести.

Проблема в том, можно ли это в принципе сделать. У меня, вроде, получилось, но при этом рухнула пара теорем. Поскольку теоремам веры больше, чем мне, то в этом месте есть проблема.