Воображаю, как я вам надоел (с)
Это последняя задача, с которой у меня проблемы. Модератор сказал разбить вопрос на две части (первая часть
тут).
Собственно, дан треугольник, заданный плоскостью -x+2y+2z-4=0. Найти циркуляцию векторного поля методом Стокса и
непосредственно. График:
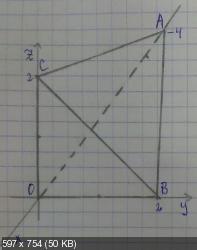
Собственно, начал решать. Так как у условии не сказано о направлении обхода, выбрал его положительным (против часовой стрелки). Сначала метод Стокса:


Вектор:

Единичный вектор:

Произведение ротора на единичный вектор:

Так как в данном случае

, достаточно лишь найти площадь треугольника

- это и будет искомой циркуляцией. Нашёл векторы треугольника:

Нашёл векторное произведение:

Длину полученного вектора:

Площадь треугольника:

Ну и циркуляцию:

Таким образом, получается, что по Стоксу циркуляция равна 9 ед. Правильно?
А вот с непосредственным вычислением у меня проблемы. Каким бы способом не решал, упорно вылезает

(иногда

).
Приведу два примера решений. Я поменял буквы у треугольника (чтобы не запутаться при вычислении циркуляции на каждом фрагменте чертежа):
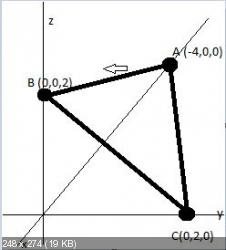
Поехали:
Способ 1.
С

небольшая проблема, пока пропущу. Уравнение прямой:


Выражаю

Получаю интеграл:

Для

Выражаю

Интегрирую

Собственно, проблема с

в том, что

и через него нельзя выразить ни

, ни

. Что я делаю не так?
Промучившить какое-то время с таким методом решения, я решил попробовать по-другому:
Способ 2.
На контуре



На контуре


На контуре


И всё равно получается ерунда.
Вопрос такой: есть ли ошибка в вычислении по методу Стокса и как правильно вычислить непосредственно? Пробовал решить ещё парой методов, тоже толком ничего не выходит.
Буду очень благодарен за подсказки.



