Задача: При движении автомобиля на подъеме с углом наклона поверхности дороги к горизонту
![$\[\beta \]$ $\[\beta \]$](https://dxdy-03.korotkov.co.uk/f/2/7/5/2752f8575bc95f27fab1de08c8e498fc82.png)
(
![$\[\sin \beta = 0.03\]$ $\[\sin \beta = 0.03\]$](https://dxdy-04.korotkov.co.uk/f/3/0/1/301864f41117c4ca81c17bc19d91935282.png)
) у него устанавливается скорость

при полезной мощности

. При движении по горизонтальной плоскости у него устанавливается скорость
![$\[\frac{3}{2}v\]$ $\[\frac{3}{2}v\]$](https://dxdy-03.korotkov.co.uk/f/2/7/d/27d695835fc95c00caff01e16a21567482.png)
при той же полезной мощности. Какую мощность

будет развивать автомобиль при спуске с углом наклона
![$\[\gamma \]$ $\[\gamma \]$](https://dxdy-03.korotkov.co.uk/f/a/3/7/a376d37d6767ef4f9e7cc8ac4e58813e82.png)
(
![$\[\sin \gamma = 0.04\]$ $\[\sin \gamma = 0.04\]$](https://dxdy-01.korotkov.co.uk/f/4/7/1/4714c69d24162b957c7136abab21099682.png)
) при скорости

. Сила сопротивления автомобилю пропорциональна квадрату его скорости.
Решение задачи получилось достаточно громоздким, вследствие чего и ответ вышел таким же. Значит в решении где-то определенно скрывается ошибка, хоть я ее и не нашел.Ах, да, ответ не зависит от

.
Решение:
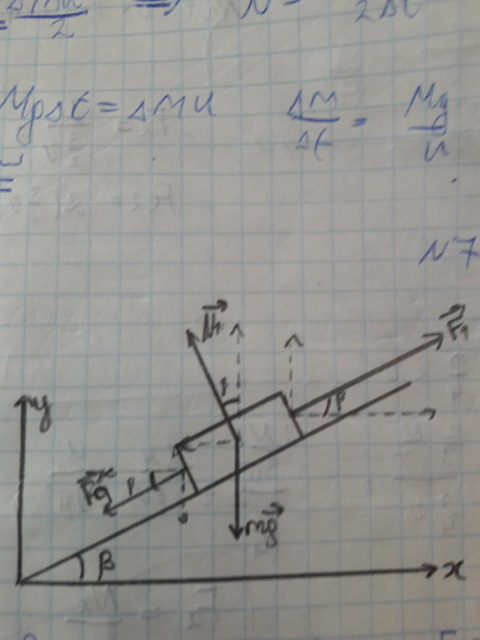
Рассмотрим первый случай. На тело действуют сила реакции опоры
![$\[\overrightarrow {{N_1}} \]$ $\[\overrightarrow {{N_1}} \]$](https://dxdy-01.korotkov.co.uk/f/c/d/9/cd9a904289480586f85560e25bfb5e1f82.png)
, сила сопротивления
![$\[\overrightarrow {{F_{c1}}} \]$ $\[\overrightarrow {{F_{c1}}} \]$](https://dxdy-03.korotkov.co.uk/f/e/8/3/e8379f13bb88fb392f0bcfce1706b7bf82.png)
, сила авто
![$\[\overrightarrow {{F_1}} \]$ $\[\overrightarrow {{F_1}} \]$](https://dxdy-03.korotkov.co.uk/f/6/1/6/6165ea8b1323dfcede982e8fd0d9de0182.png)
,сила тяжести
![$\[m\overrightarrow g \]$ $\[m\overrightarrow g \]$](https://dxdy-04.korotkov.co.uk/f/7/1/8/7189276b875019260bdf623a1b0b243282.png)
.Так как авто движется с постоянной скоростью, то имеем
![$$\[\overrightarrow {{N_1}} + \overrightarrow {{F_{c1}}} + m\overrightarrow g + \overrightarrow {{F_1}} = \overrightarrow 0 \]$$ $$\[\overrightarrow {{N_1}} + \overrightarrow {{F_{c1}}} + m\overrightarrow g + \overrightarrow {{F_1}} = \overrightarrow 0 \]$$](https://dxdy-02.korotkov.co.uk/f/9/7/8/9784c94f793cf496fa42cd4be139414282.png)
Спроецируем на ось

:
![$$\[\begin{gathered}
{N_1}\cos \beta + {F_1}\sin \beta - mg - {F_{c1}}\sin \beta = 0 \hfill \\
{N_1}\cot \beta + {F_1} - \frac{{mg}}{{\sin \beta }} - {F_{c1}} = 0 \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
{N_1}\cos \beta + {F_1}\sin \beta - mg - {F_{c1}}\sin \beta = 0 \hfill \\
{N_1}\cot \beta + {F_1} - \frac{{mg}}{{\sin \beta }} - {F_{c1}} = 0 \hfill \\
\end{gathered} \]$$](https://dxdy-03.korotkov.co.uk/f/6/5/1/6518cb5475496791b99d1aeeb1b66a8882.png)

:
![$$\[\begin{gathered}
{F_1}\cos \beta - {F_{c1}}\cos \beta - {N_1}\sin \beta = 0 \hfill \\
{F_1} - {F_{c1}} - {N_1}\tan \beta = 0 \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
{F_1}\cos \beta - {F_{c1}}\cos \beta - {N_1}\sin \beta = 0 \hfill \\
{F_1} - {F_{c1}} - {N_1}\tan \beta = 0 \hfill \\
\end{gathered} \]$$](https://dxdy-04.korotkov.co.uk/f/7/b/7/7b76cda2093867a5379327997bd775d182.png)
Итак, имеем систему:
![$$\[\left\{ \begin{gathered}
{N_1}\cot \beta + {F_1} - \frac{{mg}}{{\sin \beta }} - {F_{c1}} = 0 \hfill \\
{F_1} - {F_{c1}} - {N_1}\tan \beta = 0 \hfill \\
\end{gathered} \right.\]$$ $$\[\left\{ \begin{gathered}
{N_1}\cot \beta + {F_1} - \frac{{mg}}{{\sin \beta }} - {F_{c1}} = 0 \hfill \\
{F_1} - {F_{c1}} - {N_1}\tan \beta = 0 \hfill \\
\end{gathered} \right.\]$$](https://dxdy-01.korotkov.co.uk/f/4/9/8/498f8a642cd8fbcde8f5961e7b0f93f082.png)
![$$\[\left\{ \begin{gathered}
{N_1}\cot \beta + {F_1} - \frac{{mg}}{{\sin \beta }} - {F_{c1}} = 0 \hfill \\
{N_1} = ({F_1} - {F_{c1}})\cot \beta \hfill \\
\end{gathered} \right. \Rightarrow \]$$ $$\[\left\{ \begin{gathered}
{N_1}\cot \beta + {F_1} - \frac{{mg}}{{\sin \beta }} - {F_{c1}} = 0 \hfill \\
{N_1} = ({F_1} - {F_{c1}})\cot \beta \hfill \\
\end{gathered} \right. \Rightarrow \]$$](https://dxdy-01.korotkov.co.uk/f/8/7/9/879d0c63984dc4be39900a146c40226482.png)

![$$\[m = \frac{{\sin \beta }}{g}({F_1} - {F_{c1}})(co{t^2} + 1) = \frac{{{F_1} - {F_{c1}}}}{{g\sin \beta }}\]$$ $$\[m = \frac{{\sin \beta }}{g}({F_1} - {F_{c1}})(co{t^2} + 1) = \frac{{{F_1} - {F_{c1}}}}{{g\sin \beta }}\]$$](https://dxdy-02.korotkov.co.uk/f/1/e/f/1efe417c65ed4c3e31cb27f5da3c600882.png)
Так как
![$\[{F_1} = \frac{N}{v},{F_{c1}} = \alpha {v^2}\]$ $\[{F_1} = \frac{N}{v},{F_{c1}} = \alpha {v^2}\]$](https://dxdy-02.korotkov.co.uk/f/9/3/0/930b059ae7471626014ee5955cfae6df82.png)
,то
![$\[m = \frac{{\frac{N}{v} - \alpha {v^2}}}{{g\sin \beta }}\]$ $\[m = \frac{{\frac{N}{v} - \alpha {v^2}}}{{g\sin \beta }}\]$](https://dxdy-01.korotkov.co.uk/f/c/e/7/ce7f8df92a7bac5aa231c52f9ab7970582.png)
.
Теперь рассмотрим 2 случай, когда тело движется по горизонтальной плоскости. Так как тело движется с постоянной скоростью, то
![$$\[\overrightarrow {{N_2}} + \overrightarrow {{F_{c2}}} + m\vec g + \overrightarrow {{F_2}} = \vec 0{\text{ }}\]$$ $$\[\overrightarrow {{N_2}} + \overrightarrow {{F_{c2}}} + m\vec g + \overrightarrow {{F_2}} = \vec 0{\text{ }}\]$$](https://dxdy-02.korotkov.co.uk/f/d/f/f/dff137634f3d71e240ce1914f7f7be0582.png)
Достаточно ограничится проекцией на

:
![$$\[\begin{gathered}
{F_{c2}} = {F_2} \hfill \\
\frac{N}{{\frac{3}{2}v}} = \alpha {\left( {\frac{3}{2}v} \right)^2} \hfill \\
\frac{{2N}}{{3v}} = \frac{9}{4}\alpha {v^2} \hfill \\
\alpha = \frac{{8N}}{{27{v^3}}} \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
{F_{c2}} = {F_2} \hfill \\
\frac{N}{{\frac{3}{2}v}} = \alpha {\left( {\frac{3}{2}v} \right)^2} \hfill \\
\frac{{2N}}{{3v}} = \frac{9}{4}\alpha {v^2} \hfill \\
\alpha = \frac{{8N}}{{27{v^3}}} \hfill \\
\end{gathered} \]$$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2389b74a51fa5b693f109b2544de8bd982.png)
Теперь рассмотрим 3 случай. Для этого достаточно переделать уравнение (1) так:
![$$\[({F_{c3}} - {F_x}){\cot ^2}(360^\circ - \gamma ) + {F_{c3}} - {F_x} - \frac{{mg}}{{\sin (360^\circ - \gamma )}} = 0\]$$ $$\[({F_{c3}} - {F_x}){\cot ^2}(360^\circ - \gamma ) + {F_{c3}} - {F_x} - \frac{{mg}}{{\sin (360^\circ - \gamma )}} = 0\]$$](https://dxdy-03.korotkov.co.uk/f/6/6/7/6675d740d4b3bb09fac3e9015dafa78f82.png)
где
![$\[{F_x} = \frac{{{N_x}}}{{2v}},{F_{c3}} = \alpha {(2v)^2} = 4\alpha {v^2}\]$ $\[{F_x} = \frac{{{N_x}}}{{2v}},{F_{c3}} = \alpha {(2v)^2} = 4\alpha {v^2}\]$](https://dxdy-01.korotkov.co.uk/f/4/2/3/423f7dc6d87a0c8130c291d367bfb41d82.png)
![$$\[\left( {4\alpha {v^2} - \frac{{{N_x}}}{{2v}}} \right){\cot ^2}\gamma + 4\alpha {v^2} - {\frac{{{N_x}}}{{2v}}_x} + \frac{{mg}}{{\sin \gamma }} = 0\]$$ $$\[\left( {4\alpha {v^2} - \frac{{{N_x}}}{{2v}}} \right){\cot ^2}\gamma + 4\alpha {v^2} - {\frac{{{N_x}}}{{2v}}_x} + \frac{{mg}}{{\sin \gamma }} = 0\]$$](https://dxdy-03.korotkov.co.uk/f/a/3/2/a3279284f1d5ba75d537040542c49db382.png)
![$$\[\left( {4\alpha {v^2} - \frac{{{N_x}}}{{2v}}} \right)({\cot ^2}\gamma + 1) + \frac{{mg}}{{\sin \gamma }} = 0\]$$ $$\[\left( {4\alpha {v^2} - \frac{{{N_x}}}{{2v}}} \right)({\cot ^2}\gamma + 1) + \frac{{mg}}{{\sin \gamma }} = 0\]$$](https://dxdy-01.korotkov.co.uk/f/4/8/e/48e1e9aa4eee25bb2847bf62192caa9482.png)
![$$\[\frac{{mg}}{{\sin \gamma ({{\cot }^2}\gamma + 1)}} = \frac{{{N_x}}}{{2v}} - 4\alpha {v^2}\]$$ $$\[\frac{{mg}}{{\sin \gamma ({{\cot }^2}\gamma + 1)}} = \frac{{{N_x}}}{{2v}} - 4\alpha {v^2}\]$$](https://dxdy-03.korotkov.co.uk/f/6/f/c/6fc5768b4142ecf24568a70e117e7db882.png)
![$$\[mg\sin \gamma = \frac{{{N_x}}}{{2v}} - 4\alpha {v^2}\]$$ $$\[mg\sin \gamma = \frac{{{N_x}}}{{2v}} - 4\alpha {v^2}\]$$](https://dxdy-01.korotkov.co.uk/f/8/9/d/89dd179cbcca320230051dc5d5d6a29382.png)
![$$\[\begin{gathered}
{N_x} = 2v(mg\sin \gamma + 4\alpha {v^2}) = 2v\left( {\frac{{\frac{N}{v} - \alpha {v^2}}}{{g\sin \beta }} \cdot g\sin \gamma + 4\alpha {v^2}} \right) = 2v\left( {\left( {\frac{N}{v} - {v^2} \cdot \frac{{8N}}{{27{v^3}}}} \right) \cdot \frac{{\sin \gamma }}{{\sin \beta }} + 4{v^2} \cdot \frac{{8N}}{{27{v^3}}}} \right) = \hfill \\
2v\left( {\left( {\frac{N}{v} - \frac{{8N}}{{27v}}} \right) \cdot \frac{{\sin \gamma }}{{\sin \beta }} + \cdot \frac{{32N}}{{27v}}} \right) = 2v\frac{N}{v}\left( {\frac{{19\sin \gamma }}{{27\sin \beta }} + \frac{{32}}{{17}}} \right) = 2N\left( {\frac{{19\sin \gamma }}{{27\sin \beta }} + \frac{{32}}{{17}}} \right) \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
{N_x} = 2v(mg\sin \gamma + 4\alpha {v^2}) = 2v\left( {\frac{{\frac{N}{v} - \alpha {v^2}}}{{g\sin \beta }} \cdot g\sin \gamma + 4\alpha {v^2}} \right) = 2v\left( {\left( {\frac{N}{v} - {v^2} \cdot \frac{{8N}}{{27{v^3}}}} \right) \cdot \frac{{\sin \gamma }}{{\sin \beta }} + 4{v^2} \cdot \frac{{8N}}{{27{v^3}}}} \right) = \hfill \\
2v\left( {\left( {\frac{N}{v} - \frac{{8N}}{{27v}}} \right) \cdot \frac{{\sin \gamma }}{{\sin \beta }} + \cdot \frac{{32N}}{{27v}}} \right) = 2v\frac{N}{v}\left( {\frac{{19\sin \gamma }}{{27\sin \beta }} + \frac{{32}}{{17}}} \right) = 2N\left( {\frac{{19\sin \gamma }}{{27\sin \beta }} + \frac{{32}}{{17}}} \right) \hfill \\
\end{gathered} \]$$](https://dxdy-04.korotkov.co.uk/f/f/9/f/f9f3379a5734a06beb064f4cb70a3a8682.png) -- 24.02.2017, 22:47 --
-- 24.02.2017, 22:47 --Эта мощность в несколько раз больше

, что очень странно.
-- 24.02.2017, 22:47 --Надеюсь, ошибка в конце.



