О соотношении математики и CS

[knizhnik]

whitefox в сообщении #1186596 писал(а):

То есть теория булевых функций это, всё-таки, математика. Ну и славно.

То есть теория булевых функций и алгебраические системы функций над полями это, всё-таки, разные вещи.

Xaositect в сообщении #1186569 писал(а):

В библиографии можно увидеть кучу ссылок на советских кибернетиков (то бишь computer science).

И почему я не удивлен?

[whitefox]

knizhnik в сообщении #1186600 писал(а):

То есть теория булевых функций и алгебраические системы функций над полями это, всё-таки, разные вещи.

То есть, по Вашему, булевы функци это не тоже самое, что и функции над полем $\mathbb{F}_2$? Можете привести функцию которая принадлежит одному классу, но не принадлежит другому?

[knizhnik]

whitefox, то есть функции над полем $\mathbb{F}_2$ входят в некие алгебраические системы над этим полем. Это будет кольцо при фиксированной арности, и полукольцо при произвольной. Конечно, как примеры алгебраических систем они наименее удачны хотя бы потому, что требуют для построения некое базовое поле $\mathbb{F}_2$. Впрочем, в приступе комбинаторной эйфории эти частные случаи в курсе алгебры конечно можно упомянуть, как наименее изящные. Но теорию булевых функций в духе Яблонского с этими СДНФ, СКНФ, базисами, замыканиями лучше в математических курсах не упоминать никогда. Я снова начинаю грезить, кажется.

[Someone]

knizhnik в сообщении #1186696 писал(а):

Я снова начинаю грезить, кажется.

Вас просили не рассказать о своих грёзах, а всего навсего привести пример булевой функции, которая не является функцией над полем $\mathbb F_2$, либо, наоборот, пример функции над полем $\mathbb F_2$, которая не является булевой функцией. Так что я поддерживаю вопрос. Нас интересуют не ваши грёзы, а понимаете ли Вы, о чём говорите.

А всякие СДНФ, СКНФ и прочее — это математическая логика и, в конечном счёте, математика.

[knizhnik]

Речь шла о теориях, а не об объектах. Если вы на абсолютном серьезе предлагаете такую проверку (к моим тезисам не относящуюся), то лучше с вами это обсуждение немедленно прекратить.

Someone в сообщении #1186701 писал(а):

А всякие СДНФ, СКНФ и прочее — это математическая логика и, в конечном счёте, математика.

В таком случае и русский язык - это в конечном счете математика.

[whitefox]

knizhnik в сообщении #1186704 писал(а):

Речь шла о теориях, а не об объектах

Другими словами, Вы признаёте, что булевы функции суть тоже самое что и функции над полем $\mathbb{F}_2?$

PS Зря Вы хамите Someone. В обсуждаемых вопросах его авторитет неоспорим, Вас же здесь никто не знает. Или Вы очередной ниспровергатель?

[Sinoid]

(Оффтоп)

knizhnik в сообщении #1186704 писал(а):

В таком случае и русский язык - это в конечном счете математика.

Кстати, я читал, что методы матлогики применяются и в филологии, уж для чего конкретно, конечно, не в курсе, но тем не менее.

[knizhnik]

(Оффтоп)

whitefox, во-первых, да, разумеется, то же самое. Во-вторых, все обвинения в хамстве должны быть на чем-то основаны. У меня таких оснований вы не найдете. В-третьих, в науке авторитетов нет. Каждое положение требует проверки, независимо от того, кто и где его высказал.

[whitefox]

knizhnik в сообщении #1186751 писал(а):

да, разумеется, то же самое

Ну и славно. На этом я выхожу из данной дискуссии.

[Someone]

Sinoid в сообщении #1186748 писал(а):

Кстати, я читал, что методы матлогики применяются и в филологии, уж для чего конкретно, конечно, не в курсе, но тем не менее.

Да, я тоже где-то встречал упоминания математической лингвистики, но тоже совершенно не представляю, о чём идёт речь.

knizhnik в сообщении #1186704 писал(а):

Речь шла о теориях, а не об объектах. Если вы на абсолютном серьезе предлагаете такую проверку (к моим тезисам не относящуюся), то лучше с вами это обсуждение немедленно прекратить.

Запахло жареным? О какой проверке Вы говорите?
В любом случае, я думаю, что обсуждение этого вопроса для кое-кого будет полезным. Если модератор захочет, он имеет полное право выделить это обсуждение в отдельную тему.

Предметом изучения в математике являются логические конструкции, существующие в психике человека.

Дискретная математика, computer science — это набор математических теорий, обычно применяемых для проектирования компьютеров и анализа их работы, или используемых для разработки программного обеспечения. Сами по себе эти теории имеют дело не с железками, а именно с логическими конструкциями. Обеспечение того, чтобы компьютер работал в соответствии с этими логическими конструкциями — это технология, а не математика и даже не computer science. Тот факт, что математическая статистика применяется для анализа экономической деятельности, не означает, что математическая статистика — это не математика, а некая "экономическая наука", даже если для анализа экономики требуются какие-то специфические методы, не нужные для анализа, допустим, текстов.

knizhnik в сообщении #1186696 писал(а):

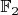
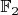
функции над полем $\mathbb{F}_2$ входят в некие алгебраические системы над этим полем. Это будет кольцо при фиксированной арности, и полукольцо при произвольной. Конечно, как примеры алгебраических систем они наименее удачны хотя бы потому, что требуют для построения некое базовое поле $\mathbb{F}_2$. Впрочем, в приступе комбинаторной эйфории эти частные случаи в курсе алгебры конечно можно упомянуть, как наименее изящные. Но теорию булевых функций в духе Яблонского с этими СДНФ, СКНФ, базисами, замыканиями лучше в математических курсах не упоминать никогда.

Тем не менее, всевозможные алгебры функций над полями, как и булевы алгебры и всякие их обобщения — стандартные алгебраические объекты, причём, изучаемые не только алгебраическими методами.

Что касается алгебры функций над полем $\mathbb F_2$ и булевой алгебры тех же функций, то есть существенные основания считать, что это один и тот же объект, только рассматриваемый немножко с разных сторон.
Рассмотрим, например, множество функций $f\colon X\to\mathbb F_2$ для некоторого непустого множества $X$.
Если мы рассматриваем это множество как алгебру функций над полем $\mathbb F_2$, то определены операции сложения $+$ и умножения $\cdot$, удовлетворяющие стандартным аксиомам ассоциативно-коммутативного кольца с нулём $\mathbf 0$ и единицей $\mathbf 1$.
Если мы рассматриваем это множество функций как булеву алгебру, то на нём определены логические операции $\vee$, $\wedge$, $\neg$ с константами $\mathbf{true}$ и $\mathbf{false}$.
Замечательный факт состоит в том, что эти два набора операций выражаются друг через друга: $f+g=(f\wedge\neg g)\vee(g\wedge\neg f)$, $f\cdot g=f\wedge g$; $f\wedge g=f\cdot g$, $f\vee g=f+g+f\cdot g$, $\neg f=f+\mathbf 1$. При этом $\mathbf{true}=\mathbf 1$ и $\mathbf{false}=\mathbf 0$.
Более того, мы можем посмотреть на ту же булеву алгебру как на частично упорядоченное множество, удовлетворяющее соответствующему набору аксиом, причём, рассмотрение этого частичного порядка будет совершенно эквивалентно рассмотрению булевой алгебры…

А Вы говорите, что булевы алгебры — это не математика, а некая computer science.

knizhnik в сообщении #1186556 писал(а):

если вы берете функции разной арности, то при естественном сложении арность результата будет максимумом из двух арностей

Это какая-то ерунда. При корректном определении должно быть совсем не так. Кроме того, мы всегда можем считать, что "арность" одинаковая, просто введя "фиктивные" аргументы.

knizhnik в сообщении #1186704 писал(а):

таком случае и русский язык - это в конечном счете математика.

Нет, русский язык, как и любой другой естественный язык — это не математика. С точки зрения математики естественный язык — это универсальный метаязык, на котором описываются все математические теории. Это не означает, что нельзя изучать этот метаязык математическими методами.

[knizhnik]

Someone в сообщении #1186794 писал(а):

Запахло жареным?

Откройте окно?

Someone в сообщении #1186794 писал(а):

О какой проверке Вы говорите?

Вы говорите, а не я.

Someone в сообщении #1186794 писал(а):

Предметом изучения в математике являются логические конструкции, существующие в психике человека.

Своеобразное определение: как минимум в нем нужно доопределить психику человека и логические конструкции. При этом ссылки на литературу, из которой вы черпаете подобные представления о математике, приветствуются, и даже абсолютно необходимы.

Someone в сообщении #1186794 писал(а):

computer science — это набор математических теорий

Для computer_scientist_ов вообще характерно весь трудный для них формализм называть "математикой". Но элементарная математика на том уровне, на котором ее понимаю я, не находит с computer science никаких пересечений. И чем дальше я продвигаюсь, тем больше это вижу.

[Sender]

(Оффтоп)

Ярошевский писал(а):

Буржуазная печать широко разрекламировала новую науку — кибернетику. Эта модная лжетеория, выдвинутая группкой американских «учёных», претендует на решение всех стержневых научных проблем и на спасение человечества от всех социальных бедствий. Кибернетическое поветрие пошло по разнообразным отраслям знания: физиологии, психологии, социологии, психиатрии, лингвистике и др. По утверждению кибернетиков, поводом к созданию их лженауки послужило сходство между мозгом человека и современными сложными машинами.

[Someone]

knizhnik в сообщении #1186811 писал(а):

Someone в сообщении #1186794 писал(а):

О какой проверке Вы говорите?

Вы говорите, а не я.

knizhnik в сообщении #1186751 писал(а):

Каждое положение требует проверки, независимо от того, кто и где его высказал.

knizhnik в сообщении #1186811 писал(а):

Someone в сообщении #1186794 писал(а):

Предметом изучения в математике являются логические конструкции, существующие в психике человека.

Своеобразное определение: как минимум в нем нужно доопределить психику человека и логические конструкции. При этом ссылки на литературу, из которой вы черпаете подобные представления о математике, приветствуются, и даже абсолютно необходимы.

Я — профессиональный математик. Мне не нужны ссылки на литературу, чтобы говорить о том, чем я занимаюсь. А формального определения математики нет и не будет.

knizhnik в сообщении #1186811 писал(а):

Но элементарная математика на том уровне, на котором ее понимаю я, не находит с computer science никаких пересечений. И чем дальше я продвигаюсь, тем больше это вижу.

Очень печально, что с таким багажом Вы лезете указывать специалистам, что есть математика, и что не есть математика.

Я думаю, что продолжение обсуждения нецелесообразно.

[knizhnik]

Someone в сообщении #1186841 писал(а):

Я — профессиональный математик. Мне не нужны ссылки на литературу, чтобы говорить о том, чем я занимаюсь.

Вы занимаетесь логическими конструкциями, существующими в психике человека? Наверное, это ближе к психологии.

Someone в сообщении #1186841 писал(а):

knizhnik в сообщении #1186811 писал(а):

Но элементарная математика на том уровне, на котором ее понимаю я, не находит с computer science никаких пересечений. И чем дальше я продвигаюсь, тем больше это вижу.

Очень печально, что с таким багажом Вы лезете указывать специалистам, что есть математика, и что не есть математика.

Наверное, по старым темам можно прикинуть мой старый уровень знаний. Но как вы его определяете на настоящий момент? Стало быть, вы определили багаж лишь исходя из того, что я не вижу как computer science относится к математике. При этом есть утверждения профессиональных математиков, которые также проводят четкие разграничения между этими науками.

Я не указываю специалистам. Я лишь высказал, что на мой взгляд в элементарных учебных курсах по математике неуместно. Все эти СКНФ, СДНФ, базисы и монотонности в духе книжки Яблонского - это пустая трата времени.

Someone в сообщении #1186841 писал(а):

Я думаю, что продолжение обсуждения нецелесообразно.

Да, ваши способы выявления багажа заставляют меня отказаться от продолжения с вами обсуждения.

[Someone]

knizhnik в сообщении #1186856 писал(а):

Я не указываю специалистам. Я лишь высказал, что на мой взгляд в элементарных учебных курсах по математике неуместно. Все эти СКНФ, СДНФ, базисы и монотонности в духе книжки Яблонского - это пустая трата времени.

Уместно или нет — зависит от конкретного курса. Кроме того, для подобных вопросов существует специальный раздел форума: "Вопросы преподавания".

knizhnik в сообщении #1186856 писал(а):

ваши способы выявления багажа

Я читаю ваши сообщения. Другого способа у меня нет.

knizhnik в сообщении #1186811 писал(а):

Для computer_scientist_ов вообще характерно весь трудный для них формализм называть "математикой".

Ну, видите же: сами специалисты по computer science говорят, что они занимаются математикой. А уж если речь пошла о формализме, то это точно математика. (Оценка трудности тех или иных математических конструкций — это личное дело каждого.)

knizhnik в сообщении #1186856 писал(а):

Вы занимаетесь логическими конструкциями, существующими в психике человека? Наверное, это ближе к психологии.

Психология не занимается изучением логических конструкций. Она интересуется самой человеческой психикой. И к математике относятся, разумеется, не все логические конструкции, существующие в человеческой психике. Но формального определения того, что относится к математике, а что — нет, не существует. А перечислить всё, что относится к математике, невозможно по причине совершенной необъятности математики в настоящее время. К тому же, завтра список придётся пополнять, а послезавтра ещё пополнять, и так далее, пока люди будут заниматься математикой и развивать её.

И где, по вашему мнению, должны существовать логические конструкции? Например, возьмём такую логическую конструкцию, как натуральное число $5$. Можно ли её найти вне человеческой психики? Если кто-то думает, что некоторый набор камешков — это и есть число $5$, то он заблуждается. Начиная уже с того, что "камешек" — это тоже не какой-то конкретный физический объект, а абстрактное понятие, то есть, логическая конструкция, существующая в человеческой психике. А физические объекты — это физические объекты, а не числа. Причём, выделение отдельных физических объектов — это опять же человеческий способ упорядочения информации об окружающем мире. В этом самом мире объекты между собой взаимодействуют, поэтому они "не очень отдельные", и их границы более или менее условные, что очень хорошо видно на микроуровне.