Xaositect, спасибо за книгу. Это похоже на довольно мощный учебник по комбинаторике. Правда он имеет слабое отношение к тому, о чем говорит
whitefox.
Правильно ли я понял, что с Вашей точки зрения теория функций над полем

это математика, а теория функций над полем
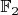
уже нет?
Нет, неправильно. Но система функций
над полем 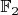
- это вообще нечто странное и неприятное. В частности, если речь только о функциях одной определенной арности, то с естественно заданными операциями мы не получаем поля. Из равенства

и свойств умножения получаем, что обе функции единичные. Откуда следует необратимость всех прочих функций.
А что с функциями над другими конечными полями?
Скорее всего, над другими конечными полями проблема сохраняется. Но если вы берете функции разной арности, то при естественном сложении арность результата будет максимумом из двух арностей. Как следствие, уже нельзя полноценно ввести противоположные элементы и вычитание.
И, вообще, с функциями над полями ненулевой характеристики?
А здесь все еще хуже. Ведь раньше мы имели дело только с конечными полями и операциями. Значит можно было просчитать все операции на компьютере или поручить ручную проверку алгебраических свойств системы каким-нибудь computer_scientist_ам. Для бесконечных (да к тому же несчетных) систем такой подход уже не сработает.
Где именно проходит грань между математикой и не математикой?
В данном случае математика заканчивается там, где мы начинаем интересоваться самыми неконцептуальными частными случаями комбинаторных объектов. При том, что применяются они не в других формальных разделах науки, а в цифровой технике и IT.