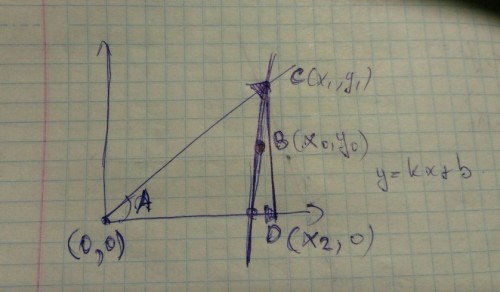
Здравствуйте! Помогите, пожалуйста с задачкой.
Задание: через точку B, лежащую внутри данного угла A провести прямую так, чтобы она отсекала от угла треугольник наименьшей площади.
Задачу надо решить именно с применением производной, не аналитически. Моя попытка решения:
Расположим систему координат так, чтобы угол

выходил из начала координат. Координаты точки

возьмем как

. Уравнение прямой, проходящей через эту точку и пересекающей две образующие угла в некоторых точках

и

, имеет вид:

, где

- неизвестный угловой коэффициент. Уравнение верхней образующей угла имеет вид:

. Уравнение нижней образующей:

.
Найдем точку пересечения

:

, откуда


. Обозначим это как

- координаты по

точки

. Тогда


.
Найдем точку пересечения

:

, откуда


, обозначим это

- координата по

точки

,

.
Тогда площадь через числовые значения проекций радиус-векторов с найденными координатами примет вид:




.
Ну а теперь самое интересное, найдя производную от этой штуки по

, получим дробь, в числителе которой будет квадратное уравнение относительно

. У меня уравнение получилось такое:

. И проблема в том, что я не знаю, как его решать. Даже знак у дискриминанта непонятно как определять. Вот и возникает вопрос: где я ошибся? Или как решить это уравнение, если все верно. Заранее спасибо.