Доброго времени, запутался в очередной раз по очень простому вопросу. Рассмотрим следующую матрицу:

,
где

- матрицы Паули.
Нужно показать, что для произвольной матрицы


тоже представимо в таком виде, причём 4-вектор

связан с

линейным преобразованием:

Вообще говоря, я понимаю, что за всем этим стоит впоследствии, но вот как это показать аккуратно, что-то не соображу. Я пытался идти "от печки": то есть тупо записал

потом перемножил

, получил конструкцию типа:

где

- 4 матрицы, коэффициенты которых выражены через коэффициенты

. Теперь имеем уже:

Можно поочередно перемножить

, подставить, объявить, что при этом
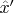
должна иметь нужный вид, после чего получить систему из четырёх уравнений. Если показать, что она разрешима относительно

, то вот и ответ получается, по сути (если к тому же ещё и решить её, то будет видно, как

связана с

). Но, как по мне, это какой-то ужасно глупый метод. Как сделать это всё элегантнее?
P.S. К слову, правильно ли я понимаю, что конкретно именно в этом задании факт того, что

, не столь важен. В том смысле, что результат может быть обощён и на более широкий класс матриц (тогда уже скалярное произведение

не будет сохраняться при преобразовании, но тут это и не требуется пока).
P.P.S. Ну и заодно уж спрошу ещё по второму заданию. Там потом просится ещё показать, что соответствующее таким

преобразование Лоренца (та самая

) может быть записано в виде

Если действовать, как выше, то, наверное, можно такой результат получить, но опять же можно как-то попроще, мне кажется. Типа воспользоваться тем, что внутри шпура можно матрицы местами переставлять, потом внимательно посмотреть на

и что-то важное осознать. Но для этого надо понять, что есть

, с чем у меня тоже затруднения, к моему стыду. Соотношение

для

я знаю, но нормально приделать сюда ещё

не могу что-то.
Заранее спасибо за помощь.



