Движение по-кругу в СТО (проверьте пожалуйста)

[Munin]

Cryo в сообщении #1170046 писал(а):

Под это определение то что я сделал подходит.

Нет, вы где-то накосячили. Потому что если взять производную, а потом проинтегрировать, должна была получиться та же самая мировая линия, а у вас ерунда получилась.

[rustot]

Cryo в сообщении #1170046 писал(а):

Вот это уже ближе! Дайте пожалуйста определение 4х скорости которое вы используете. Я думал что 4х-скорость по определению это просто производная от мировой линии обьекта по его собственному времени. Под это определение то что я сделал подходит.

Нет не походит. Дифференциал точки на мировой линии $dx^i = (c dt, dx, dy, dz)$ (либо $dx_i=(c dt, -dx, -dy, -dz)$), дифференциал собственного времени $d\tau = ds/c = \sqrt{dx^i dx_i}/c = \sqrt{dt^2- dx^2/c^2- dy^2/c^2- dz^2/c^2}$. Это все определения, нельзя вместо использования определений величин пытаться их угадать. Делите одно на другое и получаете единственно возможный результат.

[Cryo]

rustot и Munin большое спасибо за вашу помощь. Мне ещё немного не понятно. Я не пытаюсь вас переспорить, просто хочу понять как нужно делать когда dxdy не доступно. Для начала, я согласен что в первом посту задача была поставлена коряво. Теперь мне это понятно. Поэтому я попытался заново её поставить. Теперь ускорение объекта вызывается ракетой на этом же самом объекте:

Cryo в сообщении #1170046 писал(а):

Мой сценарий в том что у ускоряющегося объекта есть ракета дающая ускорение модулем в $a$. Прикреплена носом к объекту и поворачивается вокруг оси $\hat{z}$ с угловой скоростью $\omega$. Мощность не подаём. Тогда уравнение движения:

$\frac{d^{2}x^{\mu}}{d\tau^2}=(0, -a\cos(\omega\tau), -a\sin(\omega\tau), 0)$

Заметьте что так как ракета неподвижна относительно объекта то у нас пока-что везде собственное время. Теперь мы интегрируем по $\tau$ и получаем 4х-скорость, но временная компонента неизвестна (это одна из 4х констант интеграции, 3 другие принимаем нулевыми):

$u^{\mu}=\frac{dx^{\mu}}{d\tau}=(A, -\frac{a}{\omega}\sin(\omega\tau), \frac{a}{\omega}\cos(\omega\tau), 0)$



Из u^{\mu}u_{\mu}=c^2 \Rightarrow A=c\sqrt{1+(a/\omega c)^2}

Можете ли прокомментировать именно эту ситуацию?

rustot в сообщении #1170114 писал(а):

Нет не походит. Дифференциал точки на мировой линии $dx^i = (c dt, dx, dy, dz)$ (либо $dx_i=(c dt, -dx, -dy, -dz)$), дифференциал собственного времени $d\tau = ds/c = \sqrt{dx^i dx_i}/c = \sqrt{dt^2- dx^2/c^2- dy^2/c^2- dz^2/c^2}$. ...

Это я понимаю. Дальше мы вытаскиваем $dt$ из корня, получаем $d\tau =\sqrt{1- ((dx/dt)^2+(dy/dt)^2+(dz/dt)^2)/c^2}dt$, дальше $|\vec{v}|^2=((dx/dt)^2+(dy/dt)^2+(dz/dt)^2)$, и наконец

$d\tau =\sqrt{1- |\vec{v}|^2/c^2}dt=dt/\gamma$
$dt/d\tau =\gamma$

Это работает и у меня! 4х-скорость

$u^{\mu}=\frac{dx^{\mu}}{d\tau}=(c\sqrt{1+(a/\omega c)^2}, -\frac{a}{\omega}\sin(\omega\tau), \frac{a}{\omega}\cos(\omega\tau), 0)$

Тогда мировая линия:

$x^{\mu}-x^{\mu}_0=(c\sqrt{1+(a/\omega c)^2}\tau, \frac{a}{\omega^2}\cos(\omega\tau), \frac{a}{\omega^2}\sin(\omega\tau), 0)$

Смещение по мировой линии:

$dx^{\mu}=(c\sqrt{1+(a/\omega c)^2}d\tau, -\frac{a}{\omega}\sin(\omega\tau)d\tau, \frac{a}{\omega}\cos(\omega\tau)d\tau, 0)=(cdt, d\vec{r})$

Скорость для неподвижного наблюдателя:

$v=|\vec{v}|=|d\vec{r}|/dt=\frac{a}{\omega(\sqrt{1+(a/\omega c)^2})}$

Тогда

$\gamma^2=1/(1-(v/c)^2)=(1-(\frac{a}{\omega c})^2/(1+(a/\omega c)^2))^{-1}=1+(\frac{a}{\omega c})^2$
$\gamma=\sqrt{1+(\frac{a}{\omega c})^2}$

Именно это мы и видим во временной компоненте 4х-скорости. Где ошибка? Просто в таком сценарии $\omega$ это не угловая скорость в ИСО неподвижного наблюдателя.

[rustot]

Cryo в сообщении #1170125 писал(а):

Мой сценарий в том что у ускоряющегося объекта есть ракета дающая ускорение модулем в $a$

Что есть эта величина, как измерена? Через измерение координат тела относительно исо и дифференцирования или как то иначе? Относительно какой именно исо (если через координаты)?

[Cryo]

4х-ускорение это вектор (a^{\mu}=du^{\mu}/d\tau=d^{2}x^{\mu}/d\tau^2), его модуль остаётся одним и тем же в любой координатной системе. Так-что мерить можете где угодно. В ИСО в которой объект мгновенно неподвижен, 4х-ускорение будет иметь нулевую временную компоненту (a^{\mu}u_{\mu}=0) а его пространственная компонента будет равна обычному ускорению (так как скорость объекта мгновенно нулевая, и собственное время равно времени в ИСО). Верно?

[Munin]

Cryo в сообщении #1170046 писал(а):

Заметьте что так как ракета неподвижна относительно объекта то у нас пока-что везде собственное время.

Это ошибка. Собственное или не собственное - надо смотреть не относительно объекта, а относительно выбранной ИСО.

[Cryo]

rustot в сообщении #1170132 писал(а):

Что есть эта величина, как измерена? Через измерение координат тела относительно исо и дифференцирования или как то иначе? Относительно какой именно исо (если через координаты)?

Munin в сообщении #1170147 писал(а):

Это ошибка. Собственное или не собственное - надо смотреть не относительно объекта, а относительно выбранной ИСО.

Да, вы правы, здесь надо по-внимательней. Давайте я введу несколько координатых систем и попытаюсь всё разобрать.

1) $S$: ИСО неподвижного наблюдателя. Kоординаты $(ct, x, y, z)$

2) $S'$: ИСО наблюдателя который покоится относительно $S$, но повёрнут на угол $\theta$ вокруг оси z. Координаты $(ct', x', y', z)$
$\hat{x}.\hat{x'}=\cos(\theta), \quad \hat{y}.\hat{y'}=\cos(\theta), \quad \hat{z}.\hat{z'}=1$

3) $S''$: ИСО наблюдателя который ориентирован также как $S'$, но движется в направлении своей y-оси со скоростью $v$. Координаты $(ct'', x', y'', z)$

4) $\bar{S}$: СО объекта вращающегося по кругу. Модуль скорости вращения равен $v$ в ИСО $S$. Координаты $(c\tau, \bar{x}, \bar{y}, z)$. К объекту прикреплена ракета которая вращается в плоскости $\bar{x}\bar{y}$ и совершает один оборот за время $\Delta \tau=2\pi/\omega$. 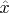$\bar{S}$ 'параллельна' $S$ в том смысле что проекции векторов $\hat{\bar{x}}$, $\hat{\bar{y}}$ в гиперплоскость $t=\operatorname{const}$ параллельны векторам $\hat{x}$, $\hat{y}$ соответственно.

Вот ориентация векторов в пространстве:


В какой-то момент $\tau=\tau_{\theta}$ 4х-скорость вращающегося объекта станет параллельна мировой линии наблюдателя покоящегося в $S''$. В частности: $(dt''/d\tau)\vert_{\tau=\tau_{\theta}}=1$

Так как обьект идёт по кругу, в момент $\tau=\tau_{\theta}$ тяга ракеты должна быть направлена в направлении $-\hat{x''}$. Следовательно 3х-ускорение в ИСО $S''$ в момент $\tau=\tau_{\theta}$ будет $\vec{a}=-a \hat{x''}=d^2 \vec{r}/dt''^2$, но так как $(dt''/d\tau)\vert_{\tau=\tau_{\theta}}=1$, то это же ускорение можно записать в пространственную часть 4х-ускорения $a^{\mu}=d^2 x^{\mu}/d\tau^2=-a{\hat{x''}}$. Временная часть ускорения отсутствует так как $a^{\mu}u_{\mu}=0$ а в момент $\tau=\tau_{\theta}$ 4х-скорость вращающегося объекта $u^{\mu}\rvert_{\tau_{\theta}}=c\hat{t''}$.

Теперь у нас есть 4х-ускорение, в момент $\tau=\tau_{\theta}$, мы его преобразуем из $S''$ в $S'$, но так как 4х-ускорение не имеет компонент в направлениях $\hat{t''}$ и $\hat{y''}$, то получаем $a^{\mu}=-a{\hat{x'}}$. Теперь надо вернуться в ИСО $S$, лабораторную систему координат, которая неподвижна относительно $S'$. Пускай $\omega\tau=\theta$ (это можно выбрать задав точку где $\tau=0$). Для перехода из $S'$ в $S$ надо повернуть пространственные части 4х-векторов на $-\theta$. Итого 4х-ускорение в базисе $S$ в момент $\tau=\tau_{\theta}$ будет $a^{\mu}=(0, -a\cos(\omega\tau), -a\sin(\omega\tau), 0)$. Момент $\tau=\tau_{\theta}$ произвольный, значит это всегда верно. Таким образом мы получили 4х-ускорение в $S$, ну а дальше нужно просто интегрировать.

[Munin]

Cryo в сообщении #1170217 писал(а):

Давайте я введу несколько координатых систем

Разберитесь хотя бы в одной, но аккуратно и начиная с определений. А нагромождая мешанину, вы же сами в ней и запутаетесь.

[Cryo]

Munin в сообщении #1170245 писал(а):

Cryo в сообщении #1170217 писал(а):

Давайте я введу несколько координатых систем

Разберитесь хотя бы в одной, но аккуратно и начиная с определений. А нагромождая мешанину, вы же сами в ней и запутаетесь.

Так я запутался или нет? Я понимаю что всё это смотреть занимает время, но вы сказали

Munin в сообщении #1170147 писал(а):

Это ошибка. Собственное или не собственное - надо смотреть не относительно объекта, а относительно выбранной ИСО.

Я попытался всё сделать аккуратно, а теперь вы не говорите ни да ни нет. Можете хотя бы посоветовать как решать ту задачу что я поставил?

[Munin]

Cryo в сообщении #1170250 писал(а):

Я попытался всё сделать аккуратно, а теперь вы не говорите ни да ни нет.

Я пока не увидел чёткого конечного результата.

Cryo в сообщении #1170250 писал(а):

Можете хотя бы посоветовать как решать ту задачу что я поставил?

И чёткой постановки задачи я тоже не увидел.

Кроме "задана мировая линия, посчитать все 4-векторы" - но это банально.

[rustot]

Cryo в сообщении #1170136 писал(а):

а его пространственная компонента будет равна обычному ускорению (так как скорость объекта мгновенно нулевая, и собственное время равно времени в ИСО). Верно?

То есть постановка задачи такая: относительно некоторой исо измерены координаты тела на каком то промежутке времени и оказалось что в момент когда первая производная становится равна нулю, вторая производная становится равной по модулю величине $a$. Также известно что мировая линия такова, что существует такая другая исо, относительно которой движение происходит по строго круговой траектории с постоянной по модулю скоростью. Найти параметры траектории в этой исо . Я правильно понял? Но тут возможно множество несовпадающих друг с другом ответов, нужно задать что то еще

[Cryo]

Мне кажется я наконец понял о чём вы говорите. Большое спасибо всем участникам темы.