Хм, да - задача сия действительно известна, но я как физик забыл об этом. Похоже сталкивался с ней в детстве, но вчера решил её забавляясь с базисами Грёбнера, что, конечно, тоже самое как стрелять с пушкой по воробьями. Сегодня узнал несколько простых решений. Есть однако и другие твердения, полученные мною тем же способом - с помощью базисами Грёбнера. Может кому-то будет интересно давать им более элегантные доказательства. Вот следующее твердение:
Пусть

площадь произвольного треугольника в котором радиусы внешне вписанных окружностей
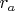
,

и

.
Докажите, что:

.
PS: Если модераторы не возражают, предлагаю изменить название топика. Пусть оно будет "Площадь треугольника выражена через..."