Macavity писал(а):
Существует более чем достаточно аксиоматик теории множеств и пока никто не доказал, какая из них самая главная.
Что значит - "главная"? Общепринятых - две (ZFC и GB). Они не эквивалентны, но разница невелика. При необходимости допускаются дополнительные аксиомы.
Macavity писал(а):
В том числе неоднократно осуществлялись попытки избавиться от бесконечностей, прийти к конструктивизму, интуицивизму и т.д. и т.п.
К теории множеств всё названное Вами имеет достаточно отдалённое отношение.
Macavity писал(а):
Сама по себе задача находится на грани фола, потому и возникают проблемы.
Элементарная задача по теории множеств, однозначно решаемая даже без формализации.
Macavity писал(а):
Someone писал(а):
Обсуждаемое построение как раз является примером такого бесконечного построения и, строго говоря, его нужно формализовать, чтобы никаких бесконечных рассуждений при этом не возникало.
Фактически здесь по индукции строится последовательность множеств

следующим образом:
1)

;
2)

при
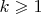
.
Задача же состоит в вычислении множества

.
Формализуя рассуждение Вы как раз и пользуетесь предельным переходом, что видно уже из Вашей формальной записи, да ещё и на индукцию ссылаетесь...
Индукция - это не предельный переход, это способ записать в конечном виде высказывание, касающееся элементов бесконечного множества. В арифметике есть специальная аксиома индукции. В теории множеств аксиомы индукции нет, потому что она является теоремой. И вообще я не понимаю, где Вы тут предельный переход увидели. Если Вы об объединении или пересечении бесконечного набора множеств, то никакого предельного перехода тут совершенно точно нет.
Macavity писал(а):
Сами по себе понятия связанные с понятием бесконечности неоднозначны в математике. Например, в евклидовой геометрии говорить о бесконечно удаленной точке не принято, её как бы и нет, а в проективной геометрии она вводится и система окресностей для бесконечно удаленной точки имеет тот же вид, что для любой другой "бесконечно неудаленной".
Вы здесь что-то путаете. Это не неоднозначность. В евклидовой геометрии не принято говорить о бесконечно удалённой точке просто потому, что в евклидовой геометрии такой точки нет, и говорить не о чем. В проективной геометрии тоже нет никакой бесконечно удалённой точки.
Macavity писал(а):
по сути "бесконечность" в каждом из случаев имеет различный смысл.
Безусловно.
Добавлено спустя 57 минут 41 секунду:AD писал(а):
Henrylee писал(а):
Разве "пустота" нижнего предела не проверяется непосредственно?
Конечно, проверяется. Только вот
Someone предложил трактовку условия, в котором на него вообще внимания не обращается ... Ну ладно, проехали, действительно.
Замечание насчёт разницы между нижним и верхним пределом было бы существенным, если бы шары, вынутые из ящика, могли в него потом возвращаться. В данном же случае однажды вынутый шар вынут навсегда, поэтому верхний и нижний пределы совпадают.
P.S. Специально для некоторых (не
AD и не
Henrylee) хочу сказать, что термины "верхний предел" и "нижний предел" для последовательности множеств

не означают никакого предельного перехода:

- множество тех элементов, которые принадлежат бесконечному семейству множеств

,

- множество тех элементов, которые принадлежат всем множествам

, кроме конечного числа.
Добавлено спустя 16 минут 38 секунд:Dan B-Yallay писал(а):
А что если не будем ложить десять шаров и вынимать один. Берем по десять из кучи, но в ящик ложим лишь 9, а номера 10,20,30 и т.д. кратные 10 - складывать возле, как будто они их только что вытащили из ящика .
Чтобы удовлетворять условиям задачи, наймем Чертика чтобы он на первом шаге
а) стер нолик у шара №10 возле ящика и превратил его в №1, затем
б) прыгнул внутрь ящика и сложенные шарики перенумеровал так, чтобы внутри были номера с 2 по 10.
На втором шаге соответственно стер нолик у шара №20 -->2 и выдал номера с 3 по 20 шарикам внутри. И вообще пусть он на каждом шаге следит за тем, чтобы чтобы нумерация шариков внутри и снаружи ящика была "правильной".
1) Сколько шариков будет в ящике по "истечении времени"?
2) Можно ли назвать хоть один номер "внутри" ящика?.
1) Бесконечное множество.
2) Нельзя.
Можно поступить ещё интереснее. Положим в ящик один шар и не будем его больше оттуда вынимать и никакие другие шары класть не будем.
На первом шаге напишем на шаре номер 1. На втором шаге этот номер сотрём и снова напишем номер 1. И вообще, на каждом шаге будем стирать написанную единицу и писать заново. Что будет написано на шаре по истечении бесконечной последовательности шагов?
Dan B-Yallay писал(а):
А еще интереснее если менять задачу не так радикально. Пусть мы складываем десять и вынимаем один как и положено. Просто в момент когда мы положили очередные десять шаров в урну, Чертик сидящий внутри мгновенно перенумеровал шарики в "обратном" порядке и мы, не зная этого, вынимаем не тот шар который нам нужен, а последний в только что положенной десятке. Будет ли такая постановка задачи парадоксом?
По-моему, такая постановка эквивалентна тому, что Вы написали выше.