Macavity писал(а):
Профессор Снэйп писал(а):
Есть такие замечательные конструкции, в которых техника перекладывания шаров по бесконечным ящикам доводится до совершенства.
Это как раз и есть гвоздь программы. Раз их много значит ими не удовлетворены.
Чем не удовлетворены? Способами перекладывания шаров? А в каком смысле ими не удовлетворены? Может быть, у тех, кто их придумывает, разные цели?
Macavity писал(а):
Someone писал(а):
Процесс описан конструктивно и однозначно, так как прямо указаны номера шаров, которые добавляются и которые удаляются, никакая аксиома выбора здесь не нужна.
Ну как же не нужна. Я приведу небольшой пример.
Не надо лучше. Вы не понимаете, что если выбираемые элементы
указаны явно, то никакие аксиомы для их выбора не нужны?
Ваших аксиом 1 и 2 в теории множеств нет. Вместо первой используется аксиома бесконечности, а вторая аксиома не нужна вообще, потому что выбор из конечного семейства (дизъюнктных) непустых множеств осуществляется без всяких аксиом: если

, то по определению

, вот его и возьмём. Для конечного семейства множеств это рассуждение нужно повторить конечное число раз. Для бесконечного же семейства множеств нужна специальная аксиома, потому что бесконечные рассуждения доказательствами не считаются, поскольку их невозможно закончить.
Обсуждаемое построение как раз является примером такого бесконечного построения и, строго говоря, его нужно формализовать, чтобы никаких бесконечных рассуждений при этом не возникало.
Фактически здесь по индукции строится последовательность множеств

следующим образом:
1)

;
2)

при
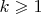
.
Задача же состоит в вычислении множества

.