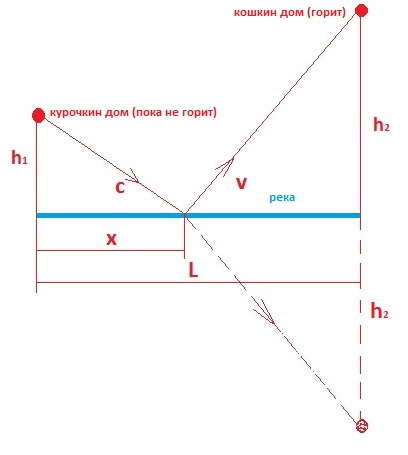
В этом случае можно, помня о принципе Ферма, сразу написать закон преломления, из которого легко находится


Как это "сразу написать закон преломления"? Ферма хоть и не знал про производные столько сколько написано в учебниках по матану, но все же применил, насколько я понимаю, аппарат бесконечно малых.
Нужны рассуждения что, как и почему. В школьном объеме. Я там выше приводил другое решение -- с веревками, грузами и кольцом. Оно дает верный ответ, и там совсем простая геометрия. Но неясно почему одну задачу можно подменить другой.
-- 06.09.2016, 17:09 --Здесь ситуация сильно облегчается тем, что корова стоит на берегу,
иначе... см. далее там же #7 (через один пост).

Но вряд ли математики одобрят такое решение...

Кстати о грузах и кольцах. Ставим чертеж с кошкиным домом горизонтально (как на рисунке ниже). На место реки крепим стержень и надеваем на него скользящее без трения кольцо.
В курочкином доме ставим блок и через него подвешиваем груз пропорциональный скорости курочки с пустым ведром, второй конец веревки привязываем к кольцу. В кошкином доме ставим блок и через него подвешиваем груз пропорциональный скорости с полным ведром, второй конец веревки привязываем к кольцу. Установившееся равновесие, наверное, и покажет оптимальный путь курочки к реке и кошкиному дому (т.е. курочке надо бежать по веревке до кольца к реке и затем от кольца к кошкиному дому).