Предел последовательности рациональных чисел конечно может быть иррациональным, и предел последовательности конечных десятичных (или двоичных) дробей может быть бесконечной дробью, но вот это Ваше утверждение неверно:
Я имел ввиду, что каждое рациональное число в двоичном (или десятичном) представлении конечно (имеет конечное число знаков, единиц, после запятой), [...]
Например, рациональное число

представляется только бесконечной дробью и в двоичной (

), и в десятичной системе (

).
Да, это я погорячился, по аналогии с натуральными числами, что конечные двоичные представления соответствуют конечным натуральным числам. Но я подумаю над разложениями дробей...
-- 12.08.2016, 15:27 --Да, мне придется согласиться с вами, теорема Кантора устояла и устояло представление Вейерштрасса, что любое вещественное число есть счетная последовательность

и

(хотя это утверждение довольно прочно зиждется на простом неравенстве, где две сходящиеся последовательности рациональных чисел отличаются на степени
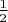
, которые при стремлении к бесконечности сводят
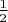
к нулю)… Действительно, множества, состоящие из счетного числа

и

, которые рассматриваю я, есть не что иное как двоичные представления натуральных чисел. И тогда мы получаем, что конечные натуральные числа соответствуют в представлении вещественных чисел (пусть от

до

) конечным двоичным последовательностям (можно рассматривать и десятичные представления), то есть конечным рациональным числам (с конечным числом двоичных или десятичных знаков), а бесконечные последовательности соответствуют вещественным числам (с бесконечным числом двоичных или десятичных знаков), - это если двоичному разложению натурального числа поставить в соответствие по цифрам знаки после запятой в двоичной дроби. И все шито-крыто. Множество всех подмножеств является континуумом.
Но последняя попытка внести большую ясность:
Для начала в моем представлении, моем отображении, между множествами всех подмножеств, или что тоже самое множеств наборов

и

, перейдем к пределу, то слева мы получим бесконечные последовательности, бесконечные подмножества, а справа бесконечно большие числа. То есть если мы от конечных последовательностей, которым соответствуют конечные числа, переходим к бесконечным последовательностям, то соответственно мы переходим и к бесконечным натуральным числам. Такова логика отрицания и построения. Вот, кстати, и в Википедии по этому поводу что-то есть, если поискать "бесконечно малая и бесконечно большая".
Теория бесконечно больших натуральных чисел или бесконечно малых рациональных чисел (только что изобрел, точнее домыслил) :
Для начала, натуральные числа бывают конечные и (вот она сила отрицания, заполняющая собой все в полноте!) и неконечные, бесконечные. Они есть как есть натуральная бесконечность. То есть все натуральные числа делятся на два класса – конечные и бесконечные. Просто вы до сих пор знали только числа из первого класса.
Вы не можете отрицать, что множество натуральных чисел бесконечно. Для обозначения бесконечности и значок существует

. Так вот это не просто бесконечность, а она имеет свою структуру и состоит из бесконечных натуральных чисел. Эти числа мы определим следующим образом: бесконечной
счетной последовательности нулей и единиц сопоставим бесконечное натуральное число, соответствующее его двоичному представлению, причем единственным образом! Тогда самым большим бесконечным числом будет

, которому будет соответствовать бесконечное натуральное число равное

, обозначим его

. Другое бесконечное число, меньшее на

-цу, выглядит так

, что соответствует

, обозначим его

, тогда разница между

и

будет как раз равна

. Причем, заметим (вот это уже круто!), что

=

, то есть

.
(К примеру еще


).
Тогда

и т.д.

.
Заметим, что бесконечные натуральные числа зависят от основания. Например, в десятичной записи, самое большое натуральное число, обозначим его

выглядит так

, то есть соответствует максимальному десятичному представлению всех натуральных чисел, тогда

Разница же между

и

равна 1.
Так вот получается новое отображение между множеством счетных последовательностей из

и

и множеством целых чисел:

– пустое множество –

.

– для всех конечных множеств берем двоичное представление конечного натурального числа.

– для всех бесконечных множеств берем двоичное бесконечное представление, что соответствует отрицательным числам в обратном порядке

– это

.
Но опять промашка, вроде, если рассмотреть

– четные числа, то опять получаем
бесконечно большие числа, но в обратном отрицательном порядке, что соответствует

То есть теорема Кантора верна, устояла!
Заметим, что бесконечно большие натуральные числа в точности соответствуют бесконечно малым рациональным числам, например, каждому бесконечно большому натуральному числу можно в точности поставить в соответствие бесконечно малое рациональное, а именно тот же набор цифр после запятой. То есть бесконечно большие натуральные числа равномощны бесконечно малым рациональным числам. То есть счетные последовательности из

и

равномощны множеству бесконечных (по разрядам в двоичном или десятичном представлении) рациональных чисел.
Можно трактовать то, что бесконечно большое (самое большое) натуральное число, равное

, говорит о том, что оно ненатурально, то есть не является конечным положительным натуральным числом. То есть, что бесконечно большие числа
ненатуральны.
Все же я опять прихожу к тому, что отрицание строится так: конечные последовательности – конечные натуральные числа, бесконечные последовательности –
ненатуральные числа, то есть как раз бесконечно малые рациональные числа, которых континуум.
Итог понимания:
1. Бесконечно малые рациональные числа представляют собой просто нерациональные – иррациональные числа. Это как раз те, у которых бесконечное число знаков после запятой в двоичном (или десятичном) представлении, как раз что соответствует бесконечным последовательностям

и

(то есть любое вещественное число зажимается делением пополам за счетное число шагов. То есть, если бы пикселы можно было делить до бесконечности, мы бы получили идеальную непрерывную картинку).
То есть счетная последовательность  и
и  задает непрерывность (это относится к пониманию бинарности, бинарной структуре мироздания, а также к бинаронсти виртуальной реальности, которая является отражением обычной реальности и стоится на двоичных битах).
задает непрерывность (это относится к пониманию бинарности, бинарной структуре мироздания, а также к бинаронсти виртуальной реальности, которая является отражением обычной реальности и стоится на двоичных битах). Конечные рациональные числа как раз соответствуют конечным последовательностям

и

и их счетное число. Кстати, также заметим, что вещественная, непрерывная прямая оказывается в биективном соответствии со всевозможными комбинациями натуральных чисел, то есть представляет собой некую всевозможную полноту. Это к вопросу о построении реальности, а именно, если взять за исходное, базовое представление вещественной прямой ее натуральный ряд (разбиение на отрезки), а потом взять всевозможные комбинации этого натурального ряда, то получим в основании вещественный ряд. То есть природа как бы заполняет все возможности, все возможные комбинации при построении. Это обнадеживает тем, что мы живем в довольно полном по возможности мире.
2. Бесконечно большие натуральные числа, которые равномощны бесконечно малым рациональным числам, то есть их континуум штук, представляют собой ненатуральные числа.
Что ж закрепили понимание. Надеюсь, другим будет уже не повадно доказывать противное теореме Кантора.
Остается квадрат и пыль Кантора. Так, я чувствую, и мое доказательство гипотезы континуума может рухнуть… и окажется, что бывает дискретный континуум, хотя бы пыль Кантора. Ну посмотрим…
Я почему так старался и пытался подвернуть разложение вещественных числе в бесконечные десятичные или двоичные представление, потому что на них основывается доказательство того, что пыль Кантора континуальна и интервал равномощен квадрату, а я вдруг иным способом доказал (ну пока что думаю, что доказал) противное. А именно:
1. Я совершенным иным, не через десятичные представления, доказал, ну или пока еще только думаю, что доказал, что интервал неравномощен квадрату.
2. Также я доказал, ну или пока еще только думаю, что доказал, гипотезу континуума, а по сути, что любое дискретное множество – счетно. Откуда следует, что Канторово множество, Канторова пыль, как дискретное множество, состоящее из отельных точек, - счетно.
Ради интереса приведу доказательство первой части (вторую, если все будет нормально, постараюсь выложить в новую тему для обсуждения, там на

страницы форума, хотя уже сам засомневался в ее верности, но поглядим):
Давайте зададимся простенькой задачкой, задачей о кеглях. Пусть у нас имеется некое количество одинаковых кеглей. Может ли это количество быть несчетным? Давайте выстроим эти кегли в ряд вдоль бесконечной прямой, длина каждой кегли фиксирована и ограничена, пусть равна

, тогда мы получаем обычный числовой ряд, который может умастить всю евклидову бесконечность, но он счетный, ибо представляет натуральную последовательность. Равно рассуждая, можно трехмерное пространство умастить счетным числом кубиков любой величины, главное, чтобы они были ненулевого объема, тогда бесконечность разбивается на счетное число частей.
Далее заметим в случае с нашими кеглями, пусть они имеют прямоугольную форму и заполняют всю бесконечность вдоль прямой, границы между ними можно подвигать как угодно, но сохраняя положительную величину, любую сколь угодно малую или сколь угодно большую длину кегли, иначе она выродится, попросту перестанет существовать. Мы можем одну кеглю растянуть как угодно вплоть до одной сплошной бесконечности, а можем сжать до размеров любого сколь угодно малого

, большего нуля, можем даже длину некоторых кеглей устремить к

. Но, что самое важное, поступая так с любой кеглей, как нам заблагорассудится, число кегель не меняется, а остается счетным, представляя разбиение бесконечности. Ибо бесконечность-то у нас одна, все та же –
.
Далее. Множество

– континуально. Действительно, если мы рассмотрим интервал

, и возьмем его

раз, то это просто можно биективно отобразить на интервал

, равный

. А далее

счетно можно устремить к бесконечности. То есть счетным числом интервалов покрыть бесконечную прямую (положительную ее часть).
Докажем, что интервал

неравномощен квадрату

.
* историческая справка: «результат о равномощности отрезка квадрату был получен в 1877 году немецким математиком Георгом Кантором и удивил его самого,
поскольку противоречил интуитивному ощущению "размерности" (квадрат двумерен, поэтому вроде бы должен содержать больше точек, чем одномерный отрезок). Вот что Кантор писал Дедекинду (20 июня 1877 года), обсуждая вопрос о равномощности пространств разного числа измерений: «Как мне кажется, на этот вопрос следует ответить утвердительно, хотя на протяжении ряда лет я придерживался противоположного мнения».
Действительно, докажем противное, единичный квадрат представляет собой континуальное, непрерывное множество единичных тел (интервалов длиной один). Наглядно это можно мыслить себе так, брать точку на оси

, по ней однозначно определяется единичный интервал вдоль оси

. У нас континуум точек на единичном интервале оси

. Мы знаем, вспоминая нашу задачу с кеглями, что
, вещественную прямую, можно умастить счетным числом единичных интервалов и только, выше мы показали, что

равномощно

(континуальному множеству). Но тогда континуальное число единичных интервалов не может поместиться на
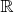
, ибо в противном случае мы получили бы счетное множество равномощно континуальному, то есть все равно, взять ли счетное число единичных тел (кеглей) или несчетное (каких не бывает вовсе в Природе размерности больше

) и умастить ими одну и туже бесконечность
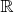
! Здесь можно возразить, что если интервал

разбить на две части, а потом на три, то

неравномощно

. Но дело в том, что мы сравниваем интервалы одинаковой длины. На интервалы одинаковой длины можно разбить интервал

единственным образом. При переходе же к счетности положительная длина утрачивает свое значение, ибо за единицу длины в этом случае мы можем брать любую длину. И в доказательстве с кеглями мы неявно использовали, что счетное множество одинаковых тел неравномощно континуальному множеству одинаковых тел, то есть просто, что счетное множество неравномощно континууму (в противном случае мы получили бы, что вещественная прямая, разрезанная на счетное число единичных интервалов, равномощна вещественной прямой, разрезанной на несчетное число интервалов, и эти одинаковые интервалы находятся в биективном соответствии просто при сопоставлении по одинаковой длине вдоль всей вещественной прямой). Грубо говоря, счетное число точек можно расширить до ненулевой ширины полосок, а несчетное нельзя*. А тогда интервал

неравномощен квадрату

. То есть множества
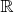
и
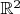
неравномощны. Аналогично доказывается и для высших размерностей. Для трехмерного случай достаточно рассмотреть ненулевые срезы плоскостей и нулевые по размеру плоскости, ну и т.д. для иных размерностей.
*Также можно доказать это иначе, а именно, если существует биекция между квадратом и прямой, то каждой точке квадрата соответствует некоторая точка на прямой, тогда рассмотрим все точки на одной полоске квадрата, что вдоль оси y и представляет континуальный интервал, ей на прямой должна соответствовать некая непрерывность, ибо все дискретные множества на прямой счетны в силу доказанного, что любое дискретное множество счетно (в чем еще предстоит увериться или опровергнуть), то есть континуальной полоске (вертикальному интервалу) должен соответствовать по крайней мере какой-то один непрерывный интервал. Полосок в квадрате несчетное число, значит на прямой должно располагаться несчетное число непересекающихся (ибо биекция) интервалов, что противоречит тому, что их может быть только счетное число.