Здравствуте, привожу условие задачи, по которой у меня возникли вопросы. С первым пунктом всё понятно, а вот со вторым не совсем. Если что, это вступительные экз. МФТИ за 94 год, 1 билет:
Цитата:
Три конденсатора с ёмкостями

,

и

, каждый из которых заряжен от батареи с ЭДС

, и резистор сопротивлением

включены в схему, изображённую на рисунке. Какая разность потенциалов установится на конденсаторе

после замыкания ключа?
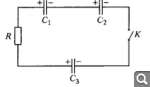
Мой ход решения: заряд из системы никуда не исчезал, а значит можно записать ЗСЗ для соотвественно положительно заряженных обкладок трех конденсаторов

(*). Также, раз в уст. режиме тока нет, то из з-на Ома следует, что

. Итого: два ур-я, три неизвестные, как связать напряжение на двух верхних конденсаторах ума не приложу.
Авторское решение:
Цитата:
Пусть конечные заряды на положительных обкладках конденсаторов соответсвенно

,

,

. Тогда ЗСЗ даст два ур-я:

,

. Также в отсутствии токов выполняется:

, решая все три уравнения получим:

Вопросы: 1)- Почему ЗСЗ должен выполняться для двух отдельных конденсаторов? Ведь на всех трех происходит перераспределение заряда, а значит из области, например, положительных обкладок 2-ого и 3-тьего конденсаторов ушёл/пришёл некоторый заряд.
2) - Подставив численные значения, которые получились у автора, получаем, что

,

, а суммарный заряд выходит равным

, что меньше исходного

(*). Что не так в моих рассуждениях?
Пожалуйста, помогите всё же восстановить истину, а то и свое решение довести не могу и чужое понять.



