Правильно понимаю, что здесь необходимо рассмотреть все случаи включения/не включения некоторого элемента

во все указанные подмножества? Для приведенного примера с тремя подмножествами таких случаев будет 8. Верно?
Рассматривать случаи можно, когда доказываем равенство множеств. Например,
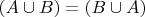
. (По первой аксиоме) для этого достаточно показать, что

. Вот он

. Значит можно рассматривать (все) случаи (4 случая):




и для каждого из них доказываете , что

тогда и только тогда, когда

(две импликации).
Вы должны доказать равносильность предложений. Для этого Вы должны доказать конъюнкцию двух импликаций.

.

.
Пока здесь элемент

не "всплыл". Есть только

.