Ориентируемость сфер и вещественных проективных пространств

[Hasek]

Надо доказать ориентируемость $S^n$ и $\mathbb{R}P^n$ при нечётных $n$.

Гладкое многообразие ориентируемо, если существует атлас, в котором якобиан перехода между любыми картами положителен.

Покроем сферу $S^n$ двумя картами: $S_+ = S^n \textbackslash (-1, 0, \ldots, 0)$ , $S_- = S^n \textbackslash (1, 0, \ldots, 0)$. Пересечением этих карт является вся сфера без северного и южного полюсов. Переход из одной карты в другую на их пересечении -- тождественное отображение. Якобиан тождественного отображения равен единице, поэтому сфера ориентируема.

На $\mathbb{R}P^n$ будем рассматривать атлас из $(n+1)$-й карты вида $U_i = \{(x^0 : x^1 : \ldots : x^n) | ~x^i \neq 0\}$. Если $x^j \neq 0$ в $i$-й карте, то координаты можно пересчитать в $j$-ю как тождественное отображение. Но вещественное проективное пространство $\mathbb{R}P^n$ ориентируемо только при нечётных $n$. Подскажите, где я не прав?

[DeBill]

Hasek в сообщении #1112868 писал(а):

Покроем сферу $S^n$ двумя картами:

А координаты то какие в этих картах? Укажите их конкретно - и вот тогда и будем посмотреть на предмет того, кто там тождественный.....

[Slav-27]

Мне интересно насчёт $\mathbb RP^2.$ Запишите явно, какие у вас карты. (Вы понимаете, что вы этого не написали?) Как вы собираетесь сделать биекцию между $\{x:y:z|x\ne0\}$ и двумерной областью и не сломает ли ваш атлас топологию?

[Brukvalub]

Немного подправим ваше доказательство и получим много больше!!!
Итак: "Покроем произвольное топологическое многообразие локальными картами $U_{\alpha}$. Пересечением этих карт является пересечение карт. Переход из одной карты в другую на их пересечении -- тождественное отображение. Якобиан тождественного отображения равен единице, поэтому каждое многообразие ориентируемо."
Ура! Я только что доказал, что неориентируемых многообразий больше нет! Долой листы Мебиуса и бутылки Кляйна!

[Hasek]

DeBill в сообщении #1112878 писал(а):

Hasek в сообщении #1112868 писал(а):

Покроем сферу $S^n$ двумя картами:

А координаты то какие в этих картах? Укажите их конкретно - и вот тогда и будем посмотреть на предмет того, кто там тождественный.....

$S^n$ находится в $\mathbb{R}^{n+1}$, поэтому давайте в качестве $n$ локальных координат брать проекции координат с $1$ по $n+1$ на гиперплоскость в $\mathbb{R}^{n+1}$ (например, легко представить для двумерной сферы -- в качестве двух локальных координат точки на сфере берём координаты её проекции на $\mathbb{R}^2$).

Slav-27 в сообщении #1112879 писал(а):

Мне интересно насчёт $\mathbb RP^2.$ Запишите явно, какие у вас карты. (Вы понимаете, что вы этого не написали?) Как вы собираетесь сделать биекцию между $\{x:y:z|x\ne0\}$ и двумерной областью и не сломает ли ваш атлас топологию?

$\mathbb{R}P^n$ можно рассматривать как $S^{n+1}$ с отождествлёнными точками, а на сфере в картах ввести локальные координаты как описано выше.

[Brukvalub]

Hasek в сообщении #1112894 писал(а):

$S^n$ находится в $\mathbb{R}^{n+1}$, поэтому давайте в качестве $n$ локальных координат брать проекции координат с $1$ по $n+1$ на гиперплоскость в $\mathbb{R}^{n+1}$ (например, легко представить для двумерной сферы -- в качестве двух локальных координат точки на сфере берём координаты её проекции на $\mathbb{R}^2$).

Во как все запущено! Это даже не биекция, так что гомеоморфизмом здесь совсем не пахнет!.

[Hasek]

Brukvalub в сообщении #1112900 писал(а):

Hasek в сообщении #1112894 писал(а):

$S^n$ находится в $\mathbb{R}^{n+1}$, поэтому давайте в качестве $n$ локальных координат брать проекции координат с $1$ по $n+1$ на гиперплоскость в $\mathbb{R}^{n+1}$ (например, легко представить для двумерной сферы -- в качестве двух локальных координат точки на сфере берём координаты её проекции на $\mathbb{R}^2$).

Во как все запущено! Это даже не биекция, так что гомеоморфизмом здесь совсем не пахнет!.

Да, действительно, ведь одним и тем же координатам будут соответствовать две точки -- одна в верхней, другая в нижней полусфере.
Понял -- при таком выборе карт лучше всего в качестве локальных координат взять координаты на плоскости стереографической проекции. Для $S_+$ это проекция из южного полюса и для $S_-$ из северного.

[Slav-27]

Hasek в сообщении #1112902 писал(а):

Понял -- при таком выборе карт лучше всего в качестве локальных координат взять координаты на плоскости стереографической проекции.

И что тогда с якобианом?

И что там с картами на $\mathbb RP^2$ -- вы ещё считаете, что получилось его ориентировать?

[Hasek]

Почти разобрался...

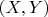
Если $(x,y,z)$ -- координаты на сфере, а $(X,Y)$ -- координаты проекции на плоскости, то имеем следующие соотношения:
$(X,Y) = (\frac{x}{1-z}, \frac{y}{1-z})$
$(x,y,z) = (\frac{2X}{1+X^2+Y^2}, \frac{2Y}{1+X^2+Y^2}, \frac{-1+X^2+Y^2}{1+X^2+Y^2})$

Пусть $\varphi_\alpha^{-1} \colon \mathbb{R}^2 \to S^2$ и $\varphi_\beta \colon S^2 \to \mathbb{R}^2$. Якобианы этих отображений имеют вид:

$D(\varphi_\beta) = \begin{pmatrix} \frac{1}{1-z} & 0 & \frac{x}{(1-z)^2}\\ 0 & \frac{1}{1-z} & \frac{y}{(1-z)^2} \end{pmatrix}$

$D(\varphi_\alpha^{-1}) = \begin{pmatrix} \frac{-2x^2+2y^2+2}{(x^2+y^2+1)^2} & \frac{-4xy}{(x^2+y^2+1)^2}\\ \frac{-4xy}{(x^2+y^2+1)^2} & \frac{2x^2-2y^2+2}{(x^2+y^2+1)^2}\\ \frac{4x}{(x^2+y^2+1)^2} & \frac{4y}{(x^2+y^2+1)^2} \end{pmatrix}$

Определитель композиции якобианов равен $\det(D(\varphi_\beta \circ \varphi_\alpha^{-1})) = - \frac{4(x^2(z+1)+y^2(z+1)-z+1)}{(z-1)^3(x^2+y^2+1)^3} > 0$.

Не до конца ещё очевидна неориентируемость $\mathbb{R}P^n$ при нечётных $n$. В интернете нашёл, что это следует из того, что антиподальное отображение на сфере чётной размерности сохраняет ориентацию, а на нечётномерной изменяет. Но как это можно понять? Похоже что это связано со степенью антиподального отображения, но мне всё ещё неочевидно.

-- 07.04.2016, 01:03 --

Даже вот так можно пересчитать.

Пусть $(x^1, x^2)$ -- координаты при проекции из северного полюса, $(y^1, y^2)$ -- из южного. Тогда они связаны соотношениями $y^1 = \frac{x^1}{(x^1)^2+(x^2)^2}$ и $y^2 = - \frac{x^2}{(x^1)^2+(x^2)^2}$.

$\det(\frac{\partial y^i}{\partial x^j}) = \frac{1}{((x^1)^2+(x^2)^2)^2} > 0$

Как понять неориентируемость чётномерных вещественных проективных пространств?

[apriv]

Hasek в сообщении #1112928 писал(а):

Как понять неориентируемость чётномерных вещественных проективных пространств?

Нарисовать клеточное разложение и посчитать старшие гомологии.

[Hasek]

apriv в сообщении #1113158 писал(а):

Hasek в сообщении #1112928 писал(а):

Как понять неориентируемость чётномерных вещественных проективных пространств?

Нарисовать клеточное разложение и посчитать старшие гомологии.

На самом деле задача предполагала решение без использования гомологий. Я разобрался так: на $\mathbb{R}P^n$ смотрим как на $S^{n+1}$, в которой антиподальное отображение задаётся $(n+1)$-й симметрией относительно гиперплоскостей, причём нечётное число симметрий изменяет (не сохраняет) ориентацию, что как раз соответствует чётной размерности вещественного проективного пространства.

Спасибо отвечавшим за помощь.