Очевидно, у обеих цепочек

и

области отправления и прибытия равны, т.к. начинаем мы всегда с

с областью отправления

, и с любым

совершаются одни и те же действия (т.е. образы в обоих случаях равны).
Вопрос не о том, какие образы. Вопрос, какие у них области прибытия (не путать с множеством значений).
Я имею в виду что правильнее будет писать так:

, где
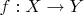
, а

Если здесь подразумеваются функции
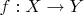
и

, где
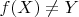
, то «перемножить» их нельзя никак. По определению.
Но если

— это частичная функция из

в

, то это просто некоторое отношение, и стрелочку в записи «

» использовать нельзя. Стрелочки уже заняты для функций.
Или вы хотите спросить, можно ли взять композицию таких отношений, что одно из них точно не функция, но получить в результате функцию. Ответ: да, можно.
В любом случае так писать неправильно.
в Википедии кстати так и написано:
В русской википедии написан феерический идиотизм в статьях, посвященных понятию функции.
Получается тогда в этом задании также не существует отображений
е)

и)

верно?
Даже в том определении композиции, которое у Давидовича, четко и недвусмысленно указаны области. Ответьте сами на этот вопрос.
-- 29.03.2016, 16:47 --Наверное, Вы имели в виду что в Вашем примере совпадают области определения (отправления)?
Я имел в виду в том примере, что совпадают и области определения (отправления), и множества значений, ибо все пустые. Но поскольку области прибытия различаются, то функции не равны, и переставлять их в композиции

нельзя.