По определению композиции из Давидовича

.
По определению композиции из Давидовича

. Можно сказать простыми словами: образ элемента при композиции равен образу образа. Ещё словами: действие композиции на элемент равно последовательному действию «функций-сомножителей».
(Оффтоп)
Мне такой подход, кстати, не нравится. Во-первых, существует удобный теоретико-множественный порядок записи композиций:

. Он полезен, если вы делаете рисунки конечных функций, располагая множества и стрелочки между ними слева направо.
Во-вторых, а что такое образ образа? Само выражение

явно не указывает на существование промежуточного элемента из некоторого промежуточного множества. Это всё попытки избежать нормального определения композиции отношений. В-третьих, а что такое

? Факт, что композиция функций — тоже функция, нетривиален, это одна из теорем, её нужно доказывать.
Короче, попытки дать теорию множеств на четырех листках ни к чему хорошему не приводят. Хотя возможно, они рассчитаны на подготовленных учеников, которые уже много знают, и которым всегда понятно о чем речь. Тогда все претензии снимаются.
Доказать, что

для любых отображений
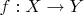
,

,

.
Ну подставьте какой-нибудь элемент (произвольный) в левую часть, и отдельно в правую часть равенства. И посмотрите что с ним происходит.
Для меня это выглядит как жонглирование обозначениями, и ничего более.
Для меня абсолютно всё, чем мы занимаемся, выглядит как жонглирование обозначениями. Теория множеств — это дисциплина гуманитарная, но вместе с тем абсолютно строгая, догматическая, православная: любое малейшее отклонение от канонов и догм может привести к ошибке.

Ну переписали мы формулу со скобками вместо кругляшков, и почему вдруг ассоциативность "появилась"?
Нужно всё свести к последовательному действию «функций-сомножителей». Кстати, у вас там ниже три примера конечных функций. Вы можете «умножить» их, не раскрывая скобок, и проверить равенство в конкретном случае.