С помощью цифрового импульсного рефлектометра произведены в одинаковых условиях измерения расстояния до места повреждения и получены результаты измерений:168,0; 169,7; 171,2; 172,3. Cлучайные погрешности имеют нормальный закон распределения c нулевым матожиданием. Найти в литературе модель измерений, согласованную с полученными результатами. Указать источник, откуда взята модель со ссылкой на номер страницы.
Придумал такую модель:
![$l_i=[10(l_0+\varepsilon_i)]/10$ $l_i=[10(l_0+\varepsilon_i)]/10$](https://dxdy-04.korotkov.co.uk/f/7/b/b/7bbf2322fb13c4630158d5b05ceb602c82.png)
, где
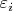
--

-я реализация случайной погрешности,

-- истинное измеряемое расстояние. Модель согласована с данными, но я испытываю трудность с источником, на который можно сослаться. Модель без округления с полученными данными не согласуется.
Подскажите, пожалуйста, как же решить заданную задачу.



