Padawan писал(а):
Гомеоморфны ли множества всех рациональных чисел и неотрицательных рациональных чисел?
Гомеоморфны. Обозначим

- множество рациональных чисел,

- множество неотрицательных рациональных чисел.
1) Функция

, где

при

, определяет гомеоморфизм множества

на множество

рациональных чисел полуинтервала
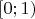
.
2) Пусть

- произвольное иррациональное число. Функция

, определяемая для

равенством

задаёт гомеоморфизм множества

на множество

.
3) Теперь мы имеем два счётных линейно упорядоченных множества

и

без первого и последнего элемента и без изолированных точек. Этих свойств достаточно, чтобы построить подобие (взаимно однозначное отображение, сохраняющее порядок)

. Поскольку топологии на

и

определяются интервалами, подобие будет гомеоморфизмом.
Подробное построение подобия немного длинно. В книге [1] (Глава IV, § 3, теорема 2) рассуждение занимает две страницы. Правда, построение ведётся без аксиомы выбора, а если её использовать, то можно и покороче.
По поводу продолжения отображения. Если

и

- полные метрические пространства,

- всюду плотное подмножество,

- непрерывное отображение, то существует его непрерывное продолжение на множество

типа

(это множество, которое можно представить как пересечение счётного семейства открытых подмножеств пространства

, содержащих

). Где посмотреть доказательство, не знаю, но идеи можно почерпнуть здесь:
http://dxdy.ru/viewtopic.php?t=337.
[1] К.Куратовский, А.Мостовский, Теория множеств, "Мир", Москва, 1970.



