Здравствуйте!
Пусть есть

экспериментов, в каждом из которых определяется

параметров. Для удобства назовём

случайную величину, соответствующую

-ому параметру в

-ом эксперименте. Требуется вычислить функцию

и найти её дисперсию.
Возможны два варианта.
Первый. В

-ом эксперименте можно оценить среднее

и дисперсию

, соответствующие случайной величине

, потом оценить взвешенное среднее и взвешенную дисперсию (усреднить по всем экспериментам), получив параметры
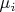
и

и вычислить функцию

на этих усреднённых оценках.
Второй вариант -- вычислить функцию

в каждом эксперименте, то есть получить набор

и соответствующих им дисперсий

, а потом оценить взвешенное среднее этих

.
В связи с этим возникает естественный вопрос: какой из двух вариантов предпочтительнее и почему?
P.S. Буду крайне благодарен за ссылки на литературу по теме.



