ins-
Попробуем разместить в кубе с ребром 9 41 шар радиуса 0.5, так, что никакая призма не пересекается с двумя шарами.
Диагональ равна 2.54, значит, пусть расстояния между центрами шаров не менее 3.54. Получили задачу: в кубе со стороной 8, отметить 41 точку так, что расстояния между точками не менее 3.54. Это равносильно: В куб со стороной 11.54, уложить 41 шар радиуса 1.77.
Ясно, что стандартная "кубическая" укладка шаров не подходит. Но есть и более экономные укладки! (гексагональная?). Переделайте уголь в алмаз!
Попробуйте, может быть, получится...
Problem 2. Можно использовать гомотетии и повороты. Но это, фактически, то же самое, что и умножение на комплексные числа...
Problem 1. Пусть

. Положим

.
Тогда

, где

.
Я люблю функцию

: если

, то легко проверить, что

.
Заметим, что

при

,

при

.
Учитывая монотонность всего, получим

. при

получим

(если я не ошибся в арифметике).
Problem 3. Индукция по

. Пусть уже есть

с нужным свойством. Пусть

- произведение этих чисел, умноженное на квадрат

- го. Увеличим все

число на

. Стало лучше! Повторив это

раз, сделаем шаг индукции.
Problem 4. Из формул для сумм кубов и квадратов, получим уравнение. У него, чудесным образом, есть натуральное решение

.
-- 28.01.2016, 19:08 --ins-
Problem 6. Точки

и

симметричны относительно прямой

, точки


-относительно прямой

. При этом, периметр вписанного треугольника с вершинами

и

, разворачивается в ломаную

, длина которой не меньше длины отрезка
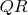
(и равна, для треугольника минимального периметра. Фактически, мы сейчас повторяем доказательство минимальности периметра вписанного для треугольника с вершинами в основаниях высот)



