svvgefest_mdПолучается, что если

, то надо показать, что

. Тогда

, т.е. функция возрастает и положительна. Это и доказывает утверждение.
И ещё вопрос:
Можно ли дифференцировать суперпозицию двух функций, если одна из них не диффиренцируема? Вроде же нет, раз нет предела в этой точке.
-- 14.01.2016, 17:11 --И ещё:
Пусть

и функция диффиренцируема в нуле. Найти
![$\lim_{h\to 0} h^{-1}\cdot [f(h)+f(h/2)+\dots +f(h/k)], k\in \mathbb{N}$ $\lim_{h\to 0} h^{-1}\cdot [f(h)+f(h/2)+\dots +f(h/k)], k\in \mathbb{N}$](https://dxdy-02.korotkov.co.uk/f/d/3/5/d35c8077a38a3adca7bcbf233d8af28082.png)
Если я умыслил, то ответ:
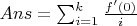 -- 14.01.2016, 17:42 --gefest_md
-- 14.01.2016, 17:42 --gefest_mdМожет у нас разные названия, но я не понимаю. Обычный алгоритм построения графика по заданной ФОРМУЛЕ:
Построить образ и прообраз, Стационарные точки, 2 производные со знаками, ассимптоты.



