Я уже говорил, что у меня туго идут доказательства --
http://dxdy.ru/post1082865.html#p1082865.
Вот опять застрял.
Определение. Пусть

— элемент некоторой группы

. Наименьшее натуральное число

такое, что
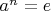
, называют порядком элемента

.
Задача. Пусть элемент

имеет порядок

. Доказать, что элементы:

все различны.
Все дело в том, что идеи какие-то есть, но не понятно правильные или ошибочные. Со своей стороны кажется, что вроде бы все хорошо. И это, наверное, естественно. Но тут же понимаю, что чего-то не хватает, может быть доказательной строгости или чего-то еще.
Например, есть такая идея доказательства этой задачи. Пусть

, то в группе

и

. Пусть

, то в группе есть элементы

и причем

, иначе бы элемент

имел порядок

. Пусть

, тогда

и

по условию и можно показать, что

, так как

, но

. И так далее по индукции для любых указанных элементов

получаем аналогичное противоречие, так как любой такой элемент всегда можно представить в виде некоторых сомножителей

, например, если мы допускаем, что

, тогда должно выполняться

, откуда получаем

и противоречие.
Помогите, пожалуйста:
во-первых разобраться с доказательством и
во-вторых, что наверное, наиболее важно, улучшить навыки доказательства, если это конечно необходимо для математического совершенствования? Хочется доказывать красиво и легко!
И
в-третьих. Хотелось бы еще понять, насколько необходимы такого рода доказательства для проникновения в определенную математическую тему. Может быть такие задачи совершенно бесполезны, как в данный момент, чтобы усвоить алгебраические группы, так и в будущем для решения математических проблем и математических исследований вообще. Если да, то что наиболее подходящее?
Следует учесть, что я занимаюсь самообразованием и времени не "вагон с тележкой". Приходится выкраивать время из обычного распорядка дня и заниматься математикой до 2-3 час. ночи, а если еще и сидеть над такими доказательствами по несколько дней, мучаться, топтаться на дном месте, то это полный швах! Хотя в качестве умственной разминки интересно.



