Сей треугольник, как можно видеть из рисунка, состоит из двух треугольников поменьше, на которые его делит диагональ

. И при таком преобразовании длина основания и высота у каждого из треугольничков как раз не меняются. А значит, не меняются их площади. А значит, не меняется площадь

как сумма их площадей. Как-то так.
Вы начинаете двигать точку

, при этом точку

тоже вынуждены двигать. При этом двигается отрезок
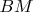
, что приводит (или не приводит - это не очевидно) к изменению основания треугольничков... Я не хочу сказать, что это не верно, я хочу сказать, что это не очевидно (по крайней мере, для меня).