В одном задачнике увидел задачу: вычислить произведение

В ответе к задаче значилось

, что легко проверяется по индукции. И если разложить разность и сумму кубов на множители и представить ответ как одну дробь, то даже понятно примерно, как можно было найти такой ответ.
Но мне сейчас интересен другой вопрос - если бы вместо сумм и разности куба и единицы стояли произвольные полиномы - всегда ли возможен был бы ответ в замкнутом виде в форме рациональной же функции?
Более формально, пусть

- полиномы (все коэффициенты - целые) одинаковой степени с одинаковым старшим членом (или даже со старшим членом единицей, неважно). Верно ли, что всегда существуют

такие, что для достаточно больших

верно

?
Для полиномов первой степени всё понятно - хотя и степень полиномов

зависит от свободного члена, что, на первый взгляд, осложняет возможность подхода к проблеме...
Если проверять, например, для данных

и

верность утверждения, то первое что приходит в голову - делать гипотезу о степени

и
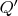
, а потом просто раскрывать скобки в рекуррентном выражении и получать систему уравнений, где в качестве неизвестных будут числа вида

(

,

- соответственно, коэффициенты

и

). Но всегда ли есть гарантия, что среди вычисленных по этой СЛАУ произведений не будет никаких противоречий?
Ну, и, конечно, даже если гипотеза не верна для всех пар полиномов, то интересно, насколько широк класс рациональных функций (и как его описать?), для произведения которых такой замкнутый вид возможен.



